#卫星导航# 3. 伪随机码

“Please,Lord,help me get one more.” –Hacksaw Ridge

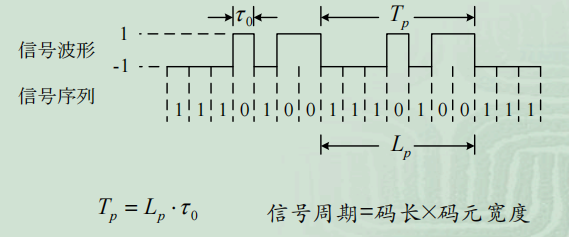
伪随机码

1. 伪随机噪声码及其主要特性

1.1 随机码和尾随机码

1. 随机码

   • 具有良好的自相关性
   • 但却是一种非周期序列，不服从任何编码规则
   • 实际无法复制使用

2. 伪随机码

   • 具有随机码序列良好相关性的有周期性的序列
   • 又具有某种确定的编码规则
   • 是周期性的
   • 容易复制

3. 二进制伪随机码

   0,1组成，简称伪码，结构可预先确定，可重复产生和复制

1.2 二进制随机码及其运算

二进制序列的运算

1. 二进制符号序列：1和0

2. 二进制信号波形：-1和1， -1表示1, 1表示0

   

3. 二进制序列的运算

   

其实就是异或运算，相同为0，不同为1。在信号波形中使用1与-1也是和这个相对应的。

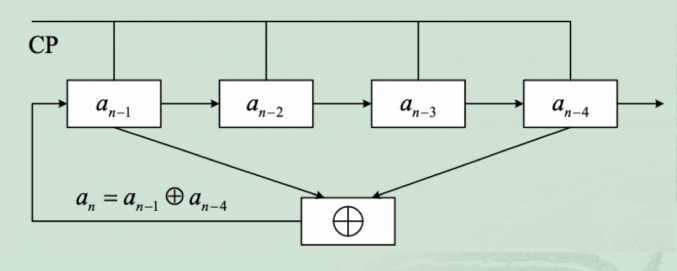
1.3 移位寄存器

伪随机码都是由“多级反馈移位寄存器”产生的，以下是一个4级移位寄存器：

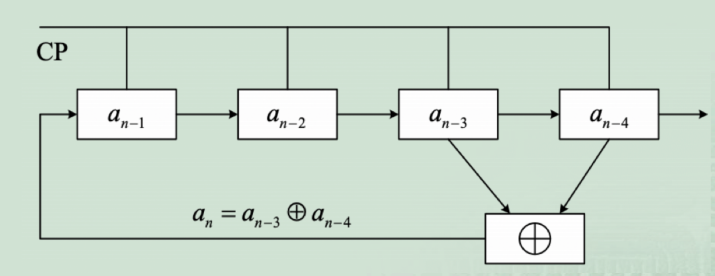\(\{a_{n-4}\}=111100010011010 \ \ \ 1111...\) 周期为15的随机序列

• 线性移位寄存器的输出序列是周期序列
• 初始状态是全0，输出也是全0
• 级数相同时，输出序列与反馈逻辑有关
• 序列周期 $ p<2^n-1 $ 的同一个线性寄存器输出与起始状态有关系（其实就是因为它一个周期内无法遍历所有非0状态）
• 序列周期 $ p=2^n-1 $ 的线性移位寄存器，输出规律与起始状态无关

1.4 最长线性移位寄存器序列——m序列

• 最大长度线性反馈移位寄存器序列（简称m序列）：线性反馈移位寄存器产生得到周期最长的二进制数字序列
• 同组m序列：相同级数不同反馈逻辑产生的m序列

特征多项式

采用特征多项式表示反馈逻辑 \(F\left( x \right) =C_0x^0+C_1x^1+C_2x^2+\cdots +C_rx^r=\sum_{i=0}^r{C_ix^i}\)

• $C_i=0$ 表示反馈线不存在
• $C_i=1$ 表示反馈线存在
• $C_0$ 始终取1

e.g. \(f(x)=x^4+x+1\) 表示如下结构的寄存器：

n级线性反馈移位寄存器能产生m序列的充要条件是它的特征多项式为一个n次本原多项式

1.5 伪随机噪声码及其应用

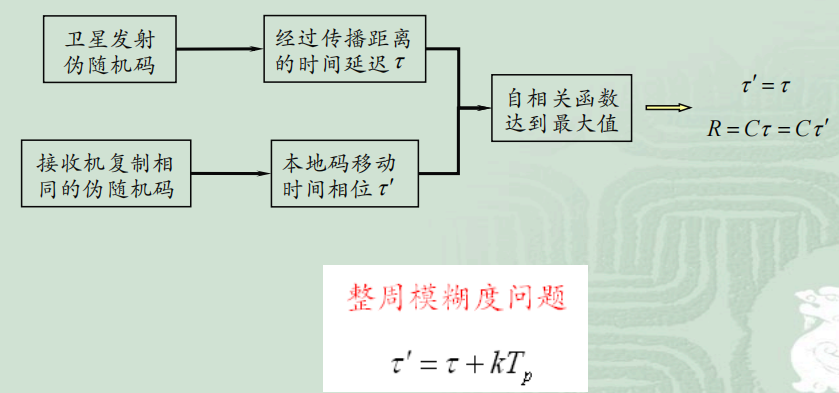
自相关特性的应用——测距

2. GPS伪随机码及其特性

• 伪随机测距码

  1. 精密测距P码

     两个码长互质m序列做模2和运算

  2. 粗捕获码，就是C/A码

     两个有良好互相关特性的同族m序列的模2和运算

• 截短码与复合码

  1. r级移位寄存器产生的m序列码长固定
  2. 实际应用中需要不同的码长序列
  3. 采用截短码或者复合码

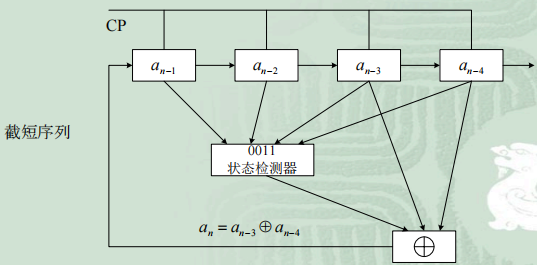
2.1 截短码

• 变成了非线性移位寄存器
• 不能用特征多项式藐视，只能用反馈逻辑函数描述

2.2 复合码

• 由两个或两个以上的短码构成一个长码成为复合码
• 一个码长为3的信号A：101 ，和另一个码长为7的信号B：1101100 ，取模2和成长码为 $3\times7=21$

\[A：101101101101101101101\] \[B：110110011011001101100\] \[A \oplus B：011011110110100000001\]

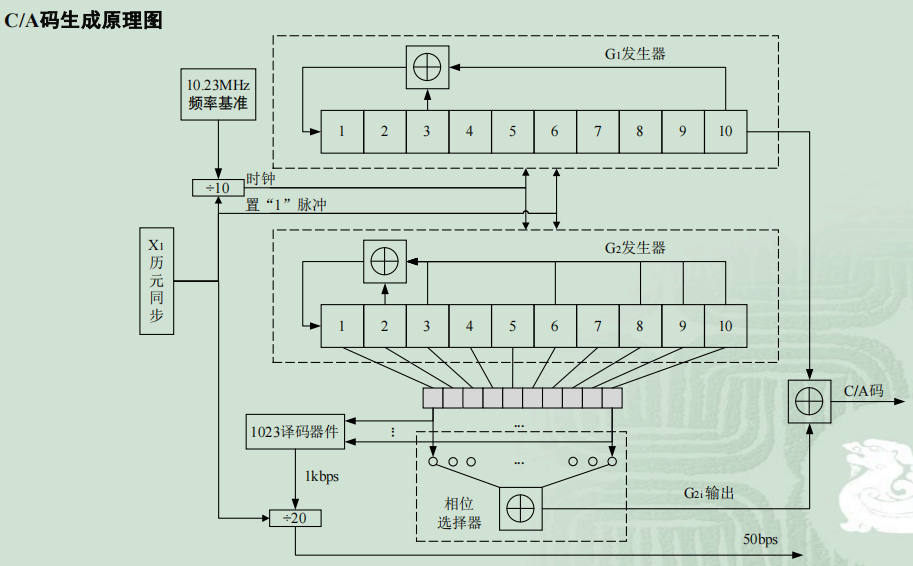
2.3 C/A码

• C/A码用于分址、搜索卫星信号和粗测距，具有一定的抗干扰能力
• 是由两个10级移位寄存器相产生
• 不同卫星有不同的C/A码
• 调制在 $L_1$ 载波
• 测距精度较低

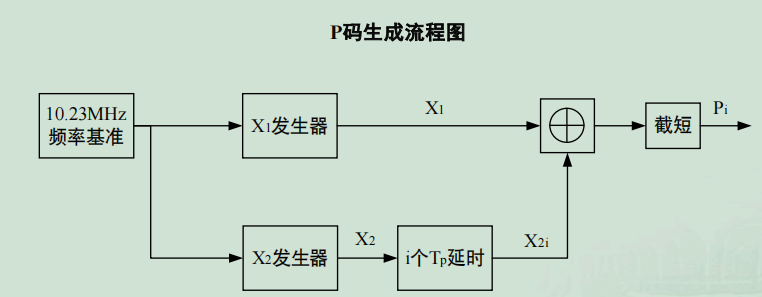
2.4 P码

• P码由两组12级反馈移位寄存器产生
• 是 $L_1,L_2$ 载波的调制信号
• 不同卫星有不同的P码
• 测距精度较高