#卫星导航# 6. 伪距定位原理

伪距定位原理

1. 伪距

1. GPS标准时间 $t$

   作为统一的时间基准保证卫星和接收机时钟的同步

2. GPS信号的发射时间 $t_s$

   \[t_s(t)=t+\delta t_s(t)\]

3. GPS信号的发射时间 $t_u$

   \[t_u(t)=t+\delta t_u(t)\]

4. 设信号从卫星到接收机所需的实际传播时间为 $\tau$，则GPS时间与卫星星钟发射时刻 $t-\tau$ 的关系为：

   \[t_s(t-\tau)=(t-\tau)+\delta t_s(t-\tau)\]

5. 测得的伪距即为：

   \[\rho(t)=c[t_u(t)-t_s(t-\tau)]\]

6. 记实际直线距离为$r$，考虑电离层延时 $I$ 与对流层延时 $T$，实际的时间

   \[\tau=\frac{r(t-\tau,t)}{c}+I+T\]

7. 将伪距的观测方程改写

   \[\rho(t)=r(t-\tau,t)+c[\delta t_u(t)-\delta t_s(t-\tau)]+cI+cT\]

​ 进一步简化，注意单位的变化

\[\rho=r+\delta t_u+\delta t_s+I+T\]

1. $\delta t_s$ 可以从第一数据块中的时钟矫正参数精确计算得到，$I$ 与 $T$ 也同样为已知量，所以对观测 $\rho$ 进行修正

   \[\rho_c=\rho+\delta t_s-I-T\]

2. 所以将未知量放在左侧，可以得到

   \[r+\delta t_u=\rho_c\]

   左侧包括接收机的三维位置与接收机钟差4个未知参数，所以当观测到4颗或以上卫星时，就可以进行解算

   \[\sqrt{(x_i-x)^2+(y_i-y)^2+(z_i-z)^2}+\delta t_u=\rho_{ci},i=1,2,3,4\]

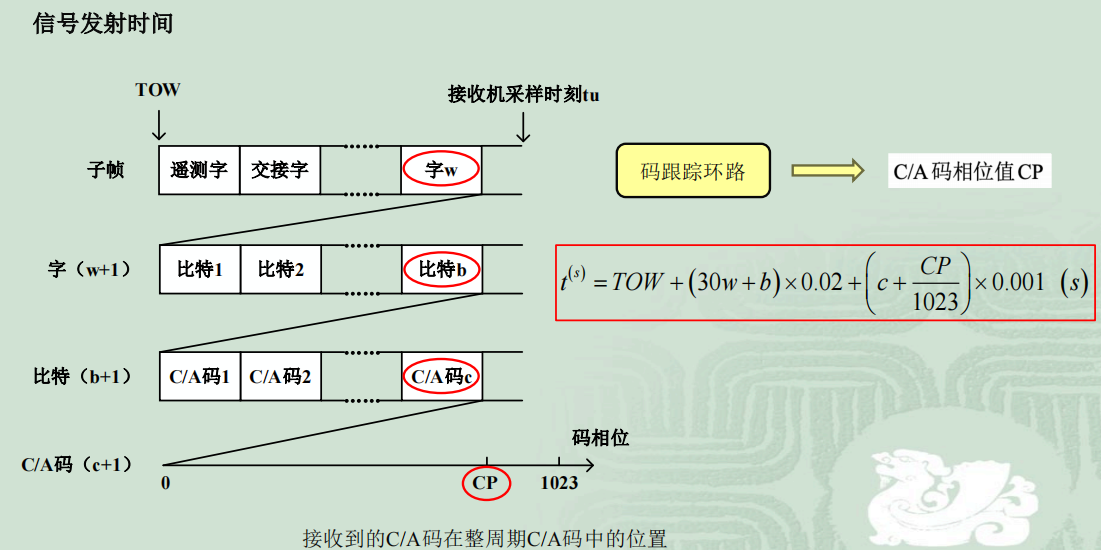
2. $t_s$ 的计算