Post

#天文导航# 天文导航总结

Posted Updated
By Young Friday
16 min read
#天文导航# 天文导航总结

天文导航总结

1. 什么是天文导航，描述天文导航的优点与不足

1.1 天文导航定义

天文导航：是以自然天体已知的准确空间为基准，通过天体测量仪器被动探测天体方位或角度，经解算确定的导航信息。

1.2 天文导航优点

  1. 天体作为天文导航的信标，没有人为干预，具有完备性和可靠性；
  2. 基于天文参考系与天文历表，其表载天体方位精确；
  3. 天体探测器接收的辐射频谱范围极宽，可覆盖X射线、紫外、可见光直至红外波段，抗干扰能力极强；
  4. 天文定姿结果的误差不随时间积累，相当于没有任何漂移的陀螺仪，适宜长期自主运行的飞行器；
  5. 同时提供姿态和位置信息；
  6. 设备简单，经济可靠，成本较低

1.3 天文导航的不足

  1. 输出数据率低，结果不连续；
  2. 在大气层内易受天气影响；

2. 什么是大圆，对于球面三角形的边和角给出准确描述，列写球面三角形的边的余弦公式和正弦公式。

声明：如果没有特别说明，所讨论的球面都是单位球面！

2.1 球和球面

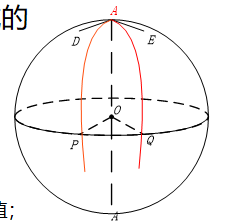
  1. 大圆

    • 大圆是指一个球面上经过球心的平面与球的交线。

    • 换句话说，大圆是球面上的最大圆，其圆心与球的圆心重合，半径等于球的半径。

  2. 球面直线、球面距离、劣弧

    • 球面直线：过球面上两点 $A,B$ 的大圆叫做过 $A,B$ 两点的球面直线
    • 球面距离：以 $A,B$ 为端点的大圆劣弧的长度

  3. 对径点、极点、极线

  4. 球面角：

    image-20241216174918463

    • 从球面上 $A$ 点出发的两个大圆半弧所构成的图形叫做球面角
    • 球面角根据二面角的大小度量
    • 顶点：两个大圆劣弧的交点
    • 边：两条大圆劣弧

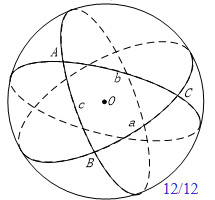
2.2 球面三角形

image-20241216174946392

  • 球面三角形：球面上不在同一大圆上的三个点 $A,B,C$ ，任两个都不是对径点，由连接 $A,B,C$ 的三条大圆劣弧组成的图形。

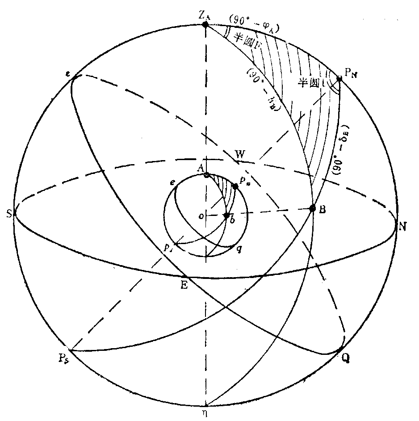
  • 导航三角形：由地球表面上北极点 $p_n$ ，观测者位置 $A$ 和天体投影点 $b$ 作为顶点，相应大圆劣弧作为其边，构成导航三角形 $\bigtriangleup Ap_nb$

  • 天文三角形：由天球表面上天北极 $P_N$ ，天体的球心投影点 $B$ 和天顶 $Z_A$ 做为顶点，和相应大圆劣弧构成的图形，称为天文三角形 $\bigtriangleup Z_AP_NB$

    image-20241216181407582

2.2.1 球面三角形性质

  1. 边的基本性质
    • 球面三角形的三边之和大于 $0$ 小于 $2\pi$
    • 球面三角形的两边之和大于第三边，两边之差小于第三边 （同平面三角形）
  2. 角的基本性质
    • 三角之和大于 $\pi$ (等腰三角，且有一个角 $\rightarrow 0$) 小于 $3\pi$ （3个平面角，三角形无限趋近于一个大圆）
    • 球面三角形两角之和减去第三角小于 $\pi$
  3. 边、角之间基本性质
    • 大边对大角
    • 大角对大边
    • 等边对等角
    • 等角对等边

2.2.2 常用公式

  1. 正弦公式

    \[\frac{\sin A}{\sin a}=\frac{\sin B}{\sin b}=\frac{\sin C}{\sin c}\]

  2. 边的余弦公式

    \[\cos a=\cos b \cos c+\sin b \sin c \cos A\]

  3. 角的余弦公式

    \[\cos A=-\cos B\cos C+\sin B \sin C \cos a\]

  4. 边的五元素公式

    \[\sin a \cos B=\cos b \sin c-\sin b \cos c \cos A\]

  5. 角的五元素公式

    \[\sin A \cos B =\cos B \sin C -\sin B \cos C \cos a\]

  6. 类勾股定理 $C=\pi/2$

    \[\cos c=\cos a\cos b\]

3. 解释太阳日长于恒星日，恒星年长于回归年的原因

3.1 太阳日长于恒星日

  • 太阳周日视运动是综合了地球自转和公转的视运动的合成效果

  • 太阳日长于恒星日

    恒星日是地球相对于恒星的自转周期，即地球自转的物理周期，是春分点的周日视运动的周期

  • 平太阳日是地球相对于平太阳的自转周期，也是平太阳的周日视运动的周期

3.2 恒星年长于回归年

  • 太阳连续两次经过瞬时平春分点的时间间隔
    • 由于岁差的作用，春分点相对于恒星逐渐向西移动，因此回归年略短于恒星年
    • 回归年的长度为约365.2422天，与季节周期相关
  • 从地球上观测，以太阳处于某一恒星的天体时圆，作为起点，当太阳再次回到这个天体时圆所经历的时长
    • 恒星年的长度为约365.2564天，与地球绕太阳的真实轨道周期对应
    • 恒星年是地球公转的实际物理周期，恒星年要长于回归年

4. 什么是儒略日和儒略世纪？

  • 儒略日：记为JD，从公园前4713年1月1日世界时12h为“0”日开始，连续不断的计日方式
  • 以回归年为基础的日历年和世纪都不是等长间隔
  • 儒略世纪：固定含有36525日，只是大时间尺度的单位，没有年和月，从1984年起作为所有天文历表的时间单位
    • 标准历元为2000年1月1.5日TT，记作 $J2000.0$ ，此时儒略日 $JD=2451545.0$
    • 儒略世纪数 $=(JD-2451545)/36525$

5. 协调世界时所联系的两个时间体制是？基本的协调方法是？

  • Universal Time Coordinated

随着世界时UT1和国际原子时TAI在时刻上偏离越来越大，日记月累的结果，TAI将与昼夜变化、生物钟以及人类作息不同步

  • UTC时间单位：原子时秒(SI)

5.1 UTC协调方法

  • 使用跳秒（闰秒）的方式，使得 $\leftUCT-UT1 \right\leqslant 0.9s$，通过天文观测不断提供差数据，一旦预测将超过 0.9s 界线，采取跳秒措施
  • 调整时刻一般在民用日历的1月1日0h或7月1日0h
    • 正跳秒：人为在0h0m0s之前加上23h59m60s——调慢1秒
    • 负跳秒：将23h59m59s 去掉，58之后紧跟0h0m0s
  • UTC和TAI的差别总是整秒

6. 什么是日月岁差？真春分点和平春分点是如何产生的？

6.1 日月岁差

  • 由于太阳、月亮和行星对地球赤道隆起部分的摄动，使得地球自转轴的方向在空间不断地运动，其中赤道平天极绕黄轴的进动被称为赤道岁差

  • 由于主要影响来自太阳（约占1/3）和月亮（约占2/3），赤道岁差通常也被称为日月岁差

  • 日月岁差不改变黄赤交角

6.2 真春分点与平春分点

  • 周期为26000年平均进动决定的春分点，不包括章动造成的短期变化
  • 由岁差和章动共同决定的春分点

7. 天文船位圆的圆心和半径各是什么？

  1. 圆心：天体与地心连线与地球表面的交点
  2. 半径：舰船到天体的天顶距

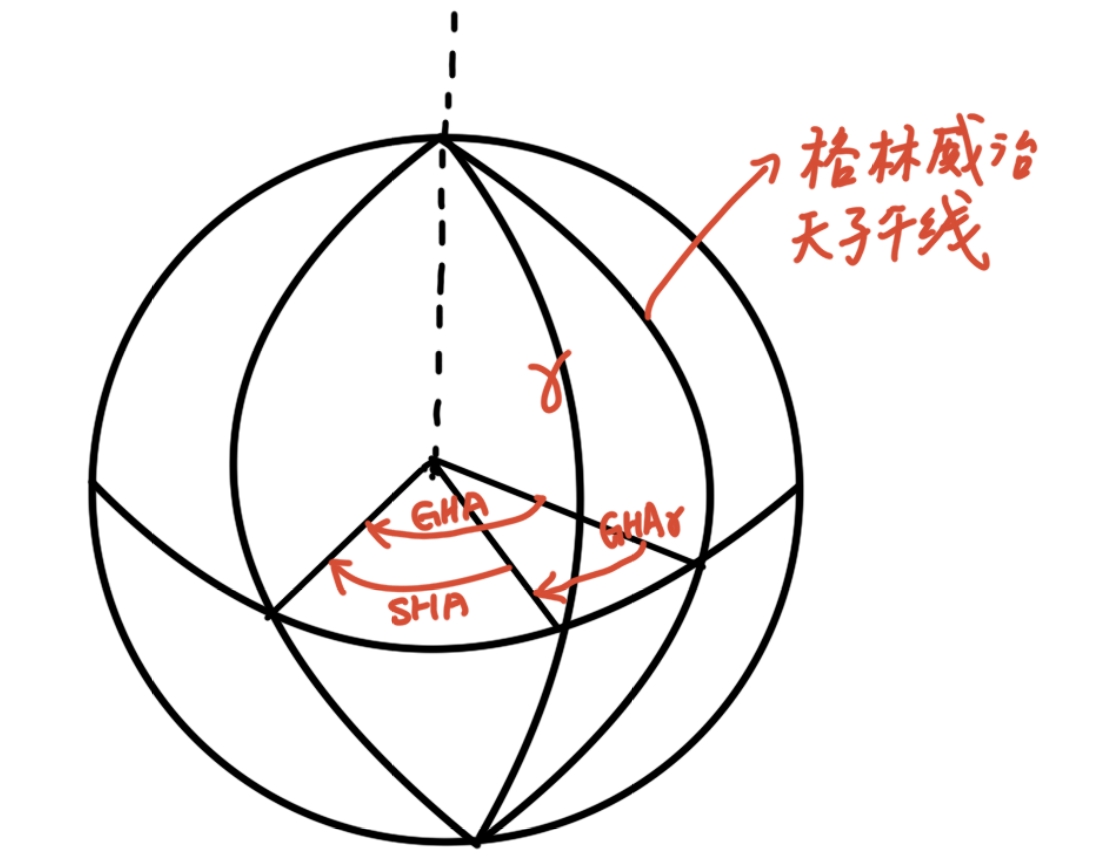
8. 请画图描述春分点时角SHA、春分点的格林时角$GHA_{\varUpsilon}$和天体的格林时角GHA，并给出三者关系的数学表达式

  • 春分点时角 $SHA$：从春分点向西道天体时圈所夹的角距，不会随地球的旋转而改变
  • 春分点格林时角 $GHA_{\varUpsilon}$
  • 格林时角 $GHA$

5d689e64830695e6919dde1a4e2803e

\[GHA=SHA+GHA_{\varUpsilon}\]

9. 地球卫星自主天文导航方法中，间接敏感地平和直接敏感地平，在基本概念内涵上有何不同，何者精度更高？

  1. 流程差异

    • 间接敏感地平同时敏感折射星光和未折射星光，得到星光折射角，再通过大气对星光折射的数学模型及补偿方法来精确敏感地平

    • 直接敏感地平敏感未折射的星光测得导航星本体坐标系下的星光矢量，再利用红外地球敏感器或空间六分仪活动本体坐标系下的地心矢量，进而计算出航天器位置等信息

  2. 可利用的星光和连续性不同

    • 间接敏感地平需要敏感折射星光，而能参与折射的星光有限，不能提供连续的观测信息

    • 直接敏感地平可以提供连续的观测信息

  3. 利用的敏感器不同

    • 间接敏感地平只使用星敏感器

    • 直接敏感地平需要使用星敏感器和红外地球敏感器或者空间六分仪

间接敏感地平精度更高，因为红外地球敏感器精度通常远低于星敏感器，导致直接敏感地平的定位精度通常不高。

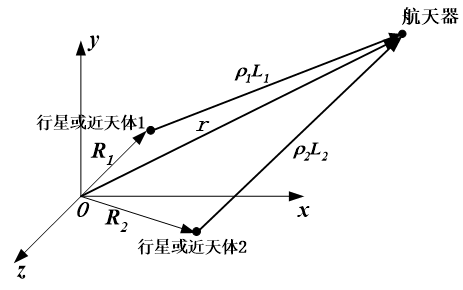
10. 列写利用2个近天体和3颗恒星之间角距测量值的天文定位几何解析法

  1. 取1行星或近天体，其到3颗恒星的单位方向矢量 $\overrightarrow{s}_i $ 已知，且测得近天体和恒星之间的星光角距，求近天体到航天器的单位方向矢量 $\overrightarrow{L_1} $

    \[\left\{\begin{matrix}L_{1}\cdot s_{1}=\cos A_{1}\\L_{1}\cdot s_{2}=\cos A_{2} \\L_{1}\cdot s_{3}=\cos A_{3}\end{matrix}\right. \left\{\begin{matrix}L_{1x}S_{1x}+L_{1y}S_{1y}+L_{1z}S_{1z}=\cos A_{1} \\L_{1x}S_{2x}+L_{1y}S_{2y}+L_{1z}S_{2z}=\cos A_{2} \\L_{1x}S_{3x}+L_{1y}S_{3y}+L_{1z}S_{3z}=\cos A_{3}\end{matrix}\right.\]

  2. 同理，换做另一颗行星，和上述同组3颗恒星或不同3颗恒星，也可确定另一条位置线 $\overrightarrow{L_2}$ ，理论上二者交汇于一点，即为航天器的位置点

  3. 设航天器位置矢量为 $\overrightarrow{r}$ ，两个行星的位置矢量分别为 $\overrightarrow{R_1},\overrightarrow{R_2}$，两行星到航天器的距离分别为 $\rho_1,\rho_2$

    image-20241219225116203

    \[\overrightarrow{r}=\overrightarrow{R_1}+\rho_1 \overrightarrow{L_1}=\overrightarrow{R_2}+\rho_2 \overrightarrow{L_2}\] \[\rho_1 \overrightarrow{L_1}-\rho_2 \overrightarrow{L_2}=\overrightarrow{R_2}-\overrightarrow{R_1}\]

    即：

    \[\left[ \begin{matrix} L_{1x}& -L_{2x}\\ L_{1y}& -L_{2y}\\ L_{1z}& -L_{2z}\\ \end{matrix} \right] \left[ \begin{array}{c} \rho _1\\ \rho _2\\ \end{array} \right] =\left[ \begin{array}{c} x_2-x_1\\ y_2-y_1\\ z_2-z_1\\ \end{array} \right]\]

  4. 使用最小二乘法确定 $\rho_1$ 与 $\rho_2$

    \[\left[ \begin{array}{c} \rho _1\\ \rho _2\\ \end{array} \right] =\left( A_{c}^{T}A_c \right) ^{-1}A_{c}^{T}\left[ \begin{array}{c} x_2-x_1\\ y_2-y_1\\ z_2-z_1\\ \end{array} \right]\]

  5. 这里介绍矩阵求逆的便捷公式，记：

    \[\overrightarrow{L_1} ·\overrightarrow{L_2}=\cos \phi\]

    则有：

    \[A_c^TA_c=\begin{bmatrix}1&-cos\phi \\-cos\phi&1\end{bmatrix},(A_c^TA_c)^{-1}=\frac{1}{sin^2\phi}\begin{bmatrix}1&cos\phi \\cos\phi&1\end{bmatrix}\]

    求解结果为：

    \[\left[ \begin{array}{c} \rho _1\\ \rho _2\\ \end{array} \right] =\frac{1}{sin^2\phi}\left[ \begin{matrix} 1& cos\phi\\ cos\phi& 1\\ \end{matrix} \right] \left[ \begin{matrix} L_{1x}& L_{1y}& L_{1z}\\ -L_{2x}& -L_{2y}& -L_{2z}\\ \end{matrix} \right] \left[ \begin{array}{c} x_2-x_1\\ y_2-y_1\\ z_2-z_1\\ \end{array} \right]\]

    则根据 $\overrightarrow{r}=\overrightarrow{R_1}+\rho_1 \overrightarrow{L_1}=\overrightarrow{R_2}+\rho_2 \overrightarrow{L_2}$ ，即可确定航天器位置。

11. 以形式最简要的流程来描述星图模拟和星光定姿的流程，注意对比两者流程的首末端

  • 星图模拟

    tianwendaohang1

    输入星敏感器姿态，输出模拟星图

  • 星光定姿

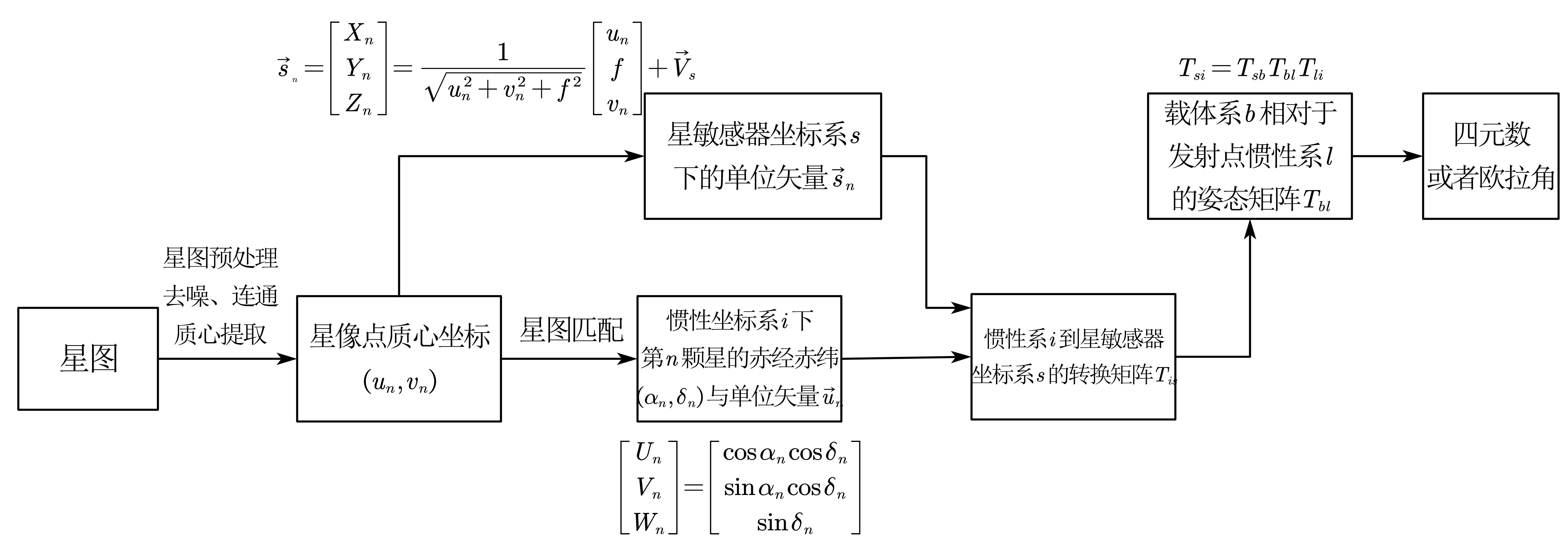
    tianwendaohang2.1

    输入星图，输出载体姿态

12. 描述基于观测多于3颗恒星实现星敏感器本体关于春分点赤道惯性系的姿态矩阵的求解方法

  1. 星图经过星图预处理、去噪、连通、质心提取后获得星像点的质心坐标$[u_1,v_1]^T$、$[u_2,v_2]^T$……$[u_n,v_n]^T$，进一步通过星图匹配获得惯性坐标系 $i$ 下单位矢量 $u_{in}$

  2. 根据星像点质心坐标计算得星敏感器坐标系 $s$ 下的单位矢量 $s_{sn}$

    \[\vec{s}_{_n}=\left[ \begin{array}{c} X_n\\ Y_n\\ Z_n\\ \end{array} \right] =\frac{1}{\sqrt{u_{n}^{2}+v_{n}^{2}+f^2}}\left[ \begin{array}{c} u_n\\ f\\ v_n\\ \end{array} \right] +\left. \vec{V}_s \right.\]

  3. 将所得坐标写成如下方程，通过最小二乘法求解惯性坐标系 $i$ 到星敏感器坐标系 $s$ 的转换矩阵 $T_{is}$

    \[\left[\begin{array}{ccc}X_1 & Y_1 & Z_1 \\ X_2 & Y_2 & Z_2 \\ & \vdots & \\ X_n & Y_n & Z_n\end{array}\right]_s=\left[\begin{array}{ccc}U_1 & V_1 & W_1 \\ U_2 & V_2 & W_2 \\ & \vdots & \\ U_n & V_n & W_n\end{array}\right]_i T_{\text {is }}=CT_{is}\]

    由最小二乘法可得：

    \[T_{is}=(C^TC)^{-1}C^TS\]
NOTES, Navigation Systems
Celestial Navigation
This post is licensed under CC BY 4.0 by the author.