#天文导航# 1. 天文导航绪论

“Love is the one thing we’re capable of perceiving that transcends dimensions of time and space.”

–Amelia Brand (Anne Hathaway), Interstellar

天文导航绪论

1. 天文导航概述

1.1 天文导航定义

天文导航：是以自然天体已知的准确空间为基准，通过天体测量仪器被动探测天体方位或角度，经解算确定的导航信息。

1.2 天文导航优点

1. 天体作为天文导航的信标，没有人为干预，具有完备性和可靠性；
2. 基于天文参考系与天文历表，其表载天体方位精确；
3. 天体探测器接收的辐射频谱范围极宽，可覆盖X射线、紫外、可见光直至红外波段，抗干扰能力极强；
4. 天文定姿结果的误差不随时间积累，相当于没有任何漂移的陀螺仪，适宜长期自主运行的飞行器；
5. 同时提供姿态和位置信息；
6. 设备简单，经济可靠，成本较低

1.3 天文导航的不足

1. 输出数据率低，结果不连续；
2. 在大气层内易受天气影响；

2. 球面三角基础知识

声明：如果没有特别说明，所讨论的球面都是单位球面！

2.1 球和球面

1. 大圆

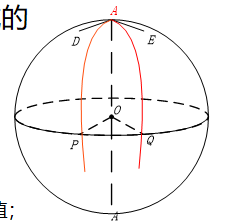
   • 大圆是指一个球面上经过球心的平面与球的交线。

   • 换句话说，大圆是球面上的最大圆，其圆心与球的圆心重合，半径等于球的半径。

2. 球面直线、球面距离、劣弧

   • 球面直线：过球面上两点 $A,B$ 的大圆叫做过 $A,B$ 两点的球面直线
   • 球面距离：以 $A,B$ 为端点的大圆劣弧的长度

3. 对径点、极点、极线

4. 球面角：

   

   • 从球面上 $A$ 点出发的两个大圆半弧所构成的图形叫做球面角
   • 球面角根据二面角的大小度量
   • 顶点：两个大圆劣弧的交点
   • 边：两条大圆劣弧

2.2 球面三角形

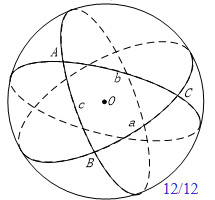
• 球面三角形：球面上不在同一大圆上的三个点 $A,B,C$ ，任两个都不是对径点，由连接 $A,B,C$ 的三条大圆劣弧组成的图形。

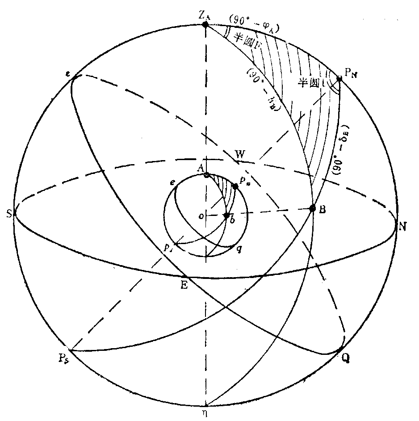
• 导航三角形：由地球表面上北极点 $p_n$ ，观测者位置 $A$ 和天体投影点 $b$ 作为顶点，相应大圆劣弧作为其边，构成导航三角形 $\bigtriangleup Ap_nb$

• 天文三角形：由天球表面上天北极 $P_N$ ，天体的球心投影点 $B$ 和天顶 $Z_A$ 做为顶点，和相应大圆劣弧构成的图形，称为天文三角形 $\bigtriangleup Z_AP_NB$

  

2.2.1 球面三角形性质

1. 边的基本性质
   • 球面三角形的三边之和大于 $0$ 小于 $2\pi$
   • 球面三角形的两边之和大于第三边，两边之差小于第三边 （同平面三角形）
2. 角的基本性质
   • 三角之和大于 $\pi$ (等腰三角，且有一个角 $\rightarrow 0$) 小于 $3\pi$ （3个平面角，三角形无限趋近于一个大圆）
   • 球面三角形两角之和减去第三角小于 $\pi$
3. 边、角之间基本性质
   • 大边对大角
   • 大角对大边
   • 等边对等角
   • 等角对等边

2.2.2 常用公式

1. 正弦公式

   \[\frac{\sin A}{\sin a}=\frac{\sin B}{\sin b}=\frac{\sin C}{\sin c}\]

2. 边的余弦公式

   \[\cos a=\cos b \cos c+\sin b \sin c \cos A\]

3. 角的余弦公式

   \[\cos A=-\cos B\cos C+\sin B \sin C \cos a\]

4. 边的五元素公式

   \[\sin a \cos B=\cos b \sin c-\sin b \cos c \cos A\]

5. 角的五元素公式

   \[\sin A \cos B =\cos B \sin C -\sin B \cos C \cos a\]

6. 类勾股定理 $C=\pi/2$

   \[\cos c=\cos a\cos b\]