#天文导航# 2. 天球坐标系

“Alright the way I see it, there’s only two possible outcomes. Either I, make it down there in one piece and I have one hell of a story to tell. Or I burn up in the next ten minutes. Either way whichever way, no harm no foul.”

–Gravity

天球坐标系

1. 基本概念

1.1 天球

• 天球是假想的一个球，以任意指定点为球心（地心、观测者的眼镜、日心、太阳系质心……），任意长为半径，这个球包容了整个宇宙的所有天体。通常，天球的半径取长度为1。

1.2 天球上的基本点、线、圆

1.2.1 天极和天赤道

• 天极：将地球自转轴无限延长与天球相交所得的直径 $P_NP_S$ ，称为天轴，两个交点分别为天北极和天南极
• 天赤道：地球赤道平面无限延伸与天球相交获得的大圆，称为天赤道 $QQ’$
• 天球的周日视运动：由于地球自转，人们感受到天球绕天轴反方向旋转，一日一周，造成天体的周日视运动

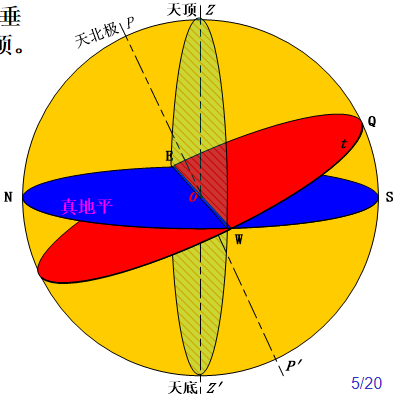
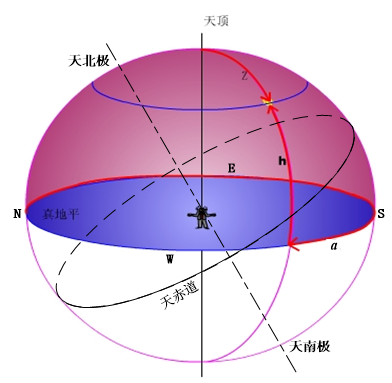
1.2.2 天顶、天底和真地平

• 天顶 $Z$ ：观测者所在地点 $A$ 的铅垂线的反向延长线与天球的交点
• 天底 $Z’$
• 真地平圈：与 $ZZ’$ 垂直的大圆 $ESWN$ 称为真地平圈。

1.2.3 天子午圈、四方点和卯酉圈

• 天子午圈：通过天顶 $Z$ 和天极 $P$ 的大圆是天子午圈，具有地方性
• 卯酉圈：过天顶，且与天子午圈垂直的大圆是卯酉圈，也具有地方性
• 四方点：天子午圈和地平圈相交与 $S$ 和 $N$ 点，靠天北极的 $N$ 为北点，靠天南极的为南点，卯酉圈与地平圈相交于 $E$ 与 $W$ 点，观测者面向北点，右方 $E$ 点称为东点，左为西点
• 天顶、天底、天子午圈、卯酉圈、四方点和地平圈都不参与天球的视运动

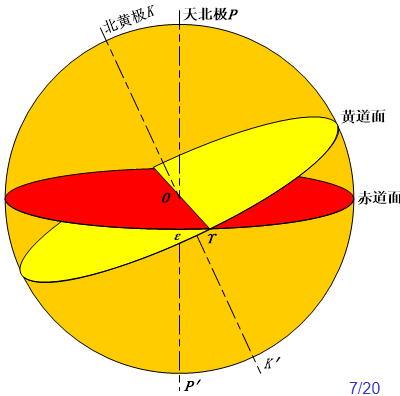
1.2.4 黄道和黄极与分至点

• 黄道：地球公转轨道投影到日心天球上的大圆，该平面就是黄道面
• 黄极：黄道有两个极，靠近天北为北黄极 $K$ ，靠近天南极为南黄极 $K’$
• 黄赤交角：黄道和赤道的交角 $\varepsilon=23°26’21’‘.488$
• 分至点：（太阳沿着黄道自西向东转，从上往下看逆时针）
  • 二分点：自南向北穿过赤道的交点是春分点 $\varUpsilon $ ，自北向南穿的是秋分点
  • 二至点：黄道上到二分点相距 $90\degree$ 的两点为二至点，赤道以北的叫夏至点，赤道以南的叫冬至点

2. 各类天球坐标系

2.1 第一赤道坐标系（时角坐标系）

• 基本大圆：天赤道
• 坐标原点：观测者子午圈和天赤道的交点 $Q$
• 时角 $t$ (地方时角LHA)：由观测者子午圈沿天赤道自东向西（顺时针，右旋） 度量至天体赤经圈$(0\sim24 \textbf{h} \ or \ 0\degree \sim 360\degree)$
• 赤纬 $\delta$：由天赤道沿过天体赤经圈向两极方向度量 $(0\degree \sim \pm 90\degree)$

与观察者位置相关，不容易统一

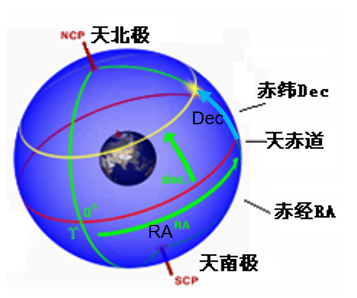
2.2 第二赤道坐标系

• 基本大圆：天赤道
• 坐标原点：春分点 $\varUpsilon $
• 赤经 $\alpha \ or \ RA$ ：由春分点沿天赤道自西向东（逆时针，左旋）度量到天体赤经圈$(0\sim24 \textbf{h} \ or \ 0\degree \sim 360\degree)$
• 赤纬 $\delta$ ：同第一赤道坐标系

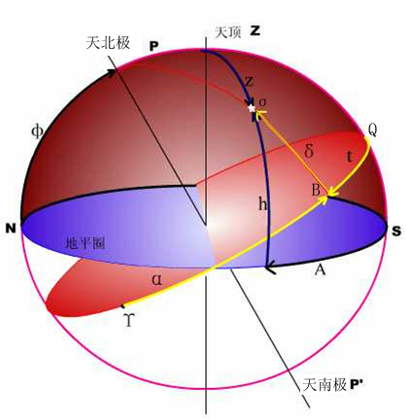
2.3 地平坐标系

• 基本大圆：地平圈
• 坐标原点：北点（或南点）
• 方位角 $\alpha$ ：从北点按照顺时针方向 $NESW\ 0\degree \sim 360\degree$ 度量
• 天体高度（仰角、高度角）$h$：由地平圈沿天体方位圆向天顶、天底量度 $0\degree \sim \pm 90\degree$
• 天顶距 $z$ ：从天顶点沿天体方位圆到天体的弧距 $(0\degree\sim180\degree)$，$z+h=90\degree$

和第一赤道坐标系一样，与观察者位置相关，不容易统一

2.4 黄道坐标系

• 基本大圆：黄道
• 坐标原点：春分点 $\varUpsilon $
• 黄经$\lambda$ ：由春分点沿黄道自西向东（逆时针，右旋），$(0\sim24 \textbf{h} \ or \ 0\degree \sim 360\degree)$ 度量到天体黄经圈
• 黄纬 $\beta$ ：由黄道沿过天体黄经圈向两极点方向度量 $(0\degree \sim \pm 90\degree)$

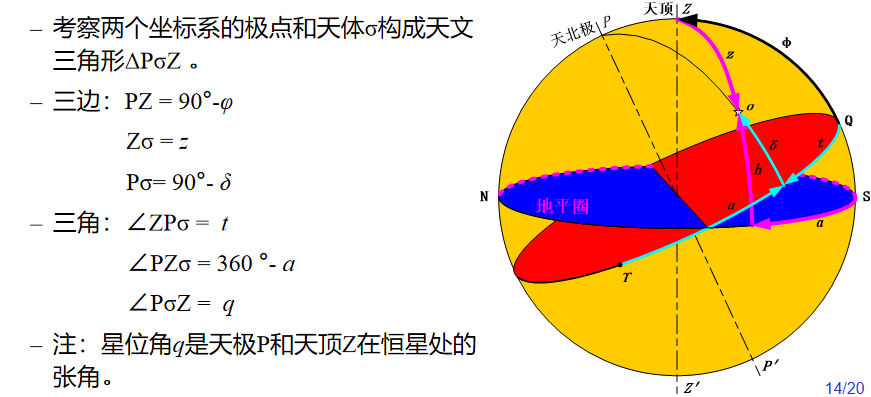
2.5 地平坐标系和时角坐标系的坐标变换

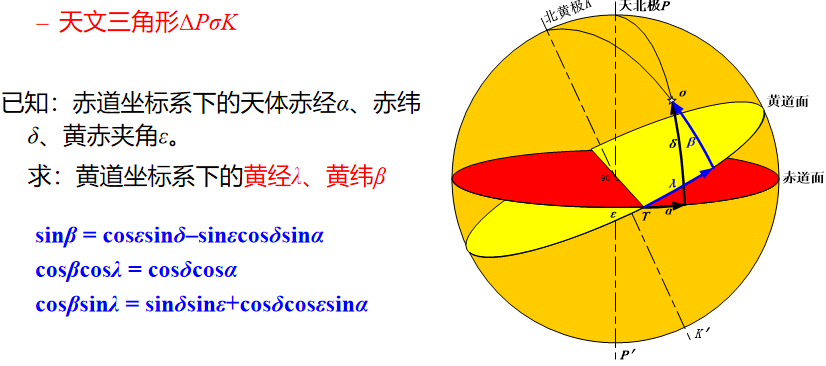
2.6 第二赤道坐标系和黄道坐标系的变换

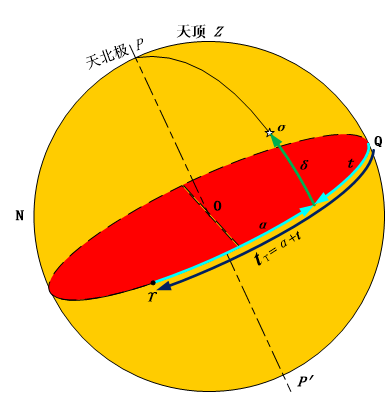
2.7 时角坐标系和第二赤道坐标系的坐标变换

• 两者有共同的赤纬坐标 $\delta$
• 时角 $t$ 和赤经 $\alpha$ 之间的联系：$t_T=\alpha+t$，其中 $t_T$ 就是地方恒星时 $s$。