#惯性导航# 3. 坐标系漫谈

3. 坐标系漫谈

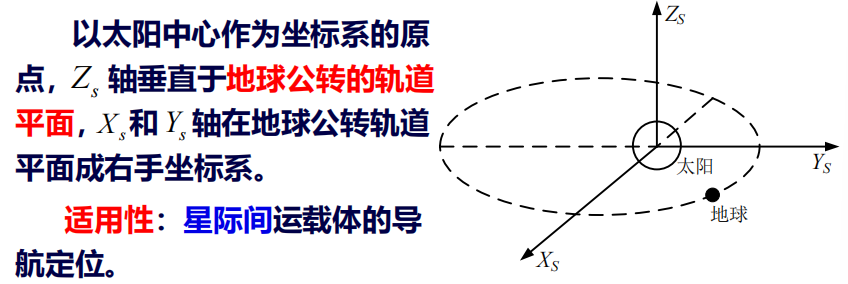
1. 惯性参考坐标系

宇宙空间保持静止或匀速直线运动为参照物构成的参照坐标系，就称为惯性参照系

（由于万有引力等因素，真实的惯性系是不存在的）

1. 太阳中心惯性坐标系

   

2. 地心惯性坐标系

   

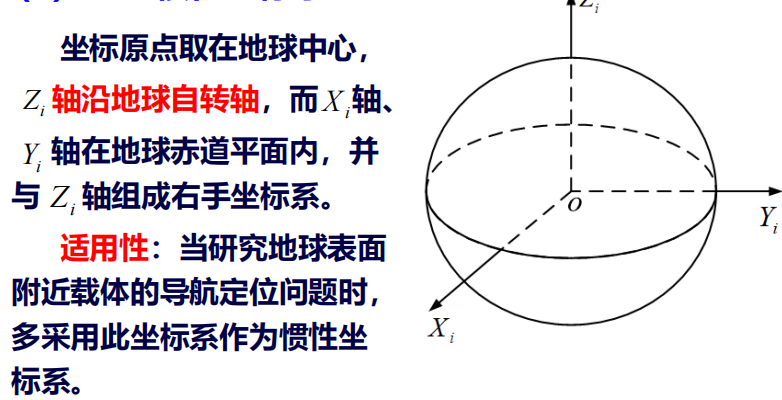
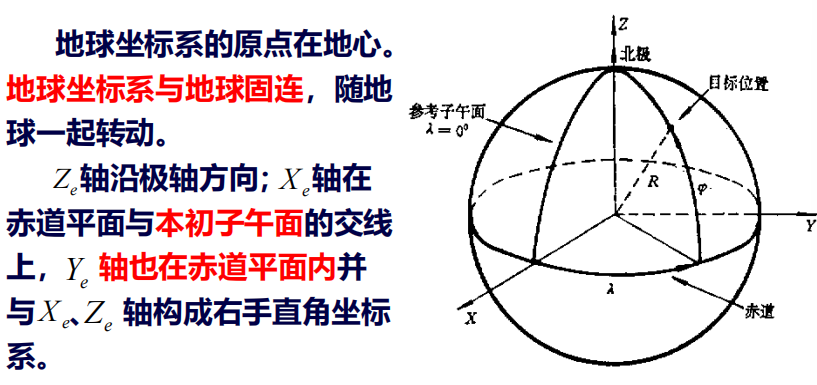
2. 地球坐标系

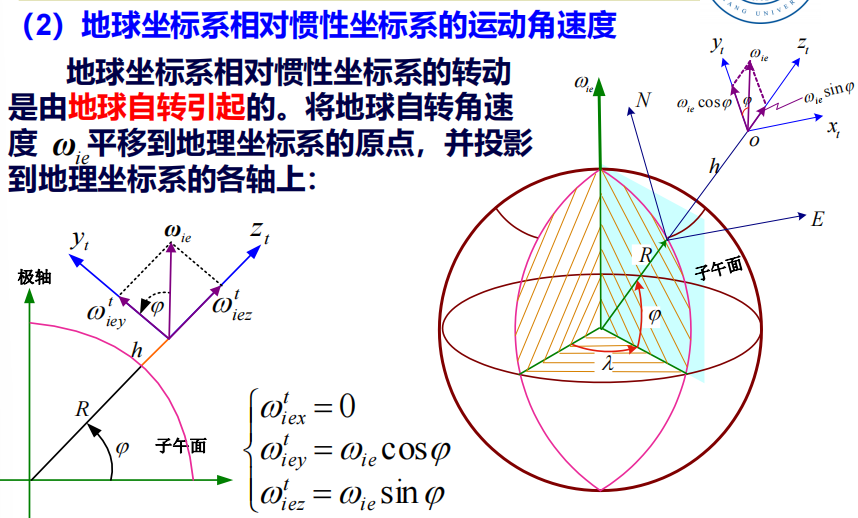
随地球一起转动$\rightarrow$ 非惯性系

地球相对于恒星（惯性空间）自转角速度，要大于地球相对太阳的自转角速度

（原因在与相对太阳坐标系分析地球自转角速度$\omega$时，需要再减去地球公转旋转角速度$\omega^{\prime}$）

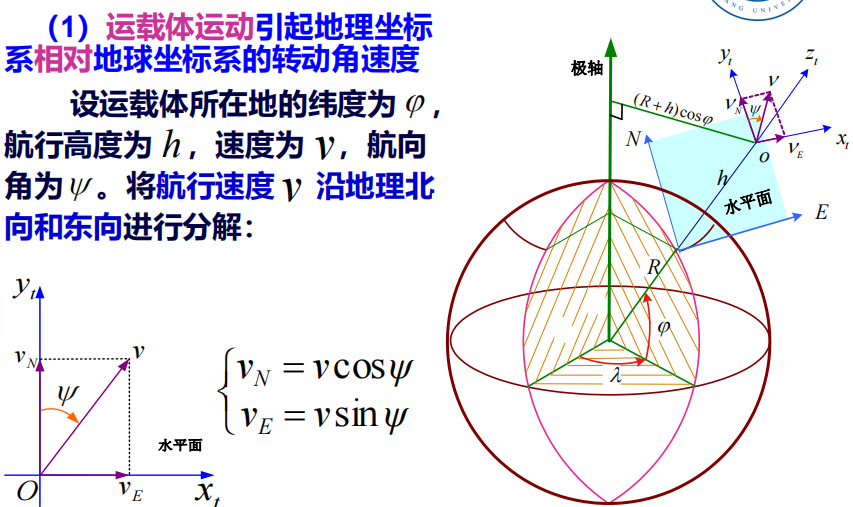
3. 地理坐标系

运载体相对地球的运动将相当于地理坐标系相对地球坐标系运动（转动）

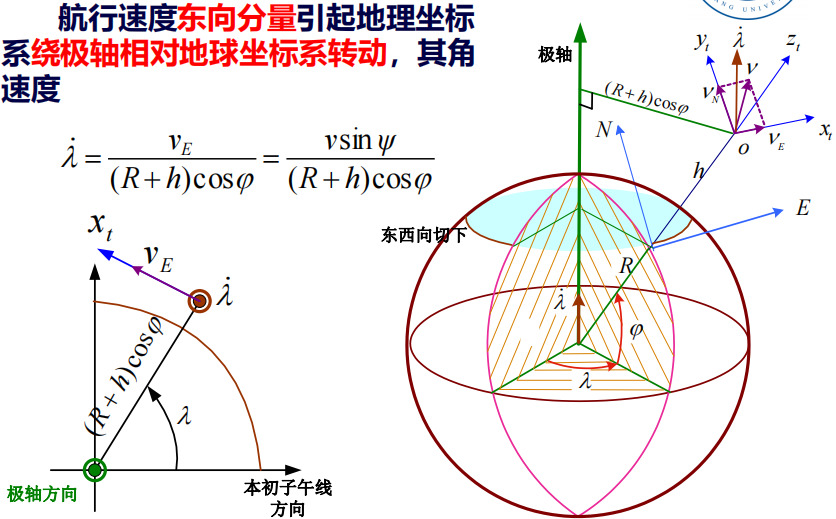
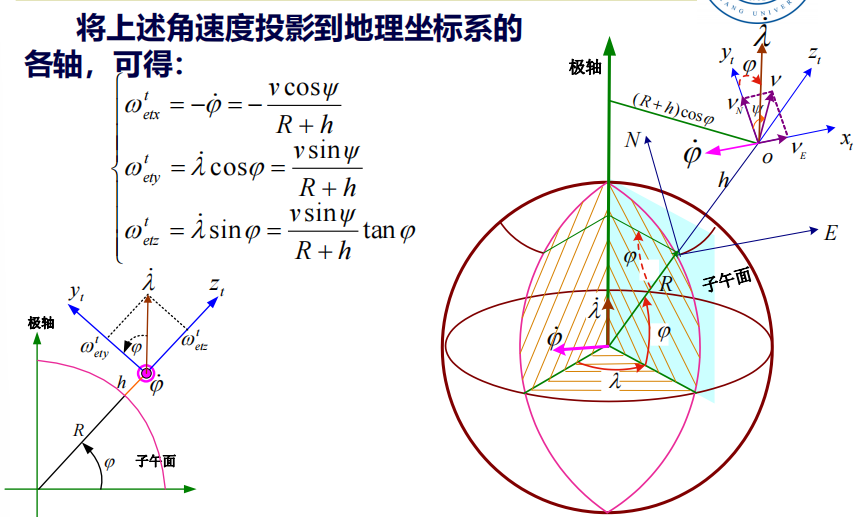
\[\omega_{地理\rightarrow 惯性}=\omega_{地理\rightarrow地球}+\omega_{地球\rightarrow 惯性}\]

1. 地理坐标系相对地球坐标系

   

   

   

   

2. 地球坐标系相对惯性坐标系

   

3. 最终地理坐标系相对惯性坐标系

   

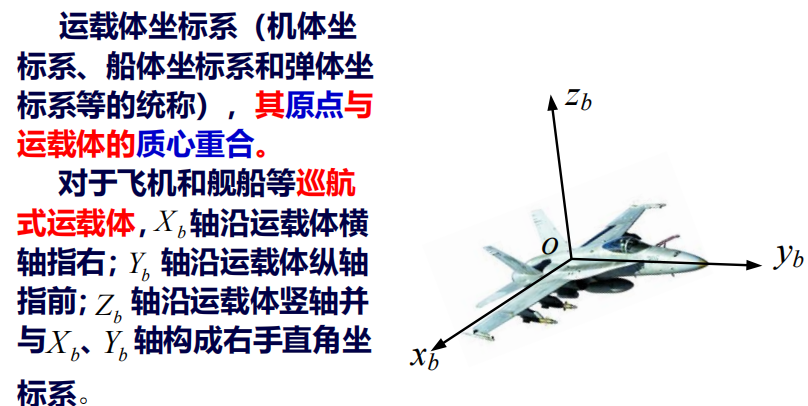
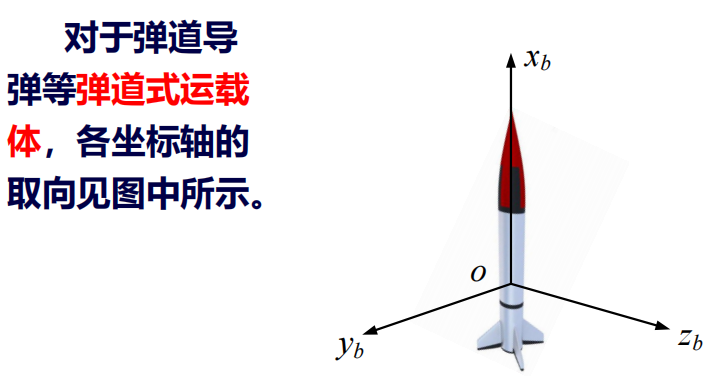
4. 载体坐标系

要点：机头对 $y$

要点：弹头对 $x$

运载体的俯仰角、横滚角和航向角统称为姿态角。姿态角是更具运载体坐标系相对地理坐标系的转角决定的 。

1. 航向角 $\psi$

   地理坐标系 $y_t$ 与载体坐标系横滚轴 $y_b$ 在水平面的投影 $y_h$ 的夹角，偏东为正

2. 俯仰角$\theta$

   $y_b$ 与 $y_h$ 的夹角，抬头为正（高于水平面）

3. 横滚角 $\gamma $

   $x_b$ 与其在水平面投影 $x_h$ 的夹角，右倾为正，左倾为负

5. 描述刚体角位置的方法

方向余弦法

1. 方向余弦

   

   \[R_x=\cos <\vec{R},\vec{i}>\\ R_y=\cos <\vec{R},\vec{j}>\\ R_z=\cos<\vec{R},\vec{k}>\]

2. 两个坐标系之间的方向余弦

   \[\left[ \begin{array}{c} R_{x}^{0}\\ R_{y}^{0}\\ R_{z}^{0}\\ \end{array} \right] =\left[ \begin{matrix} \cos \left( \boldsymbol{i}_{_r},\boldsymbol{i}_{_0} \right)& \cos \left( \boldsymbol{j}_{_r},\boldsymbol{i}_{_0} \right)& \cos \left( \boldsymbol{k}_{_r},\boldsymbol{i}_{_0} \right)\\ \cos \left( \boldsymbol{i}_{_r},\boldsymbol{j}_{_0} \right)& \cos \left( \boldsymbol{j}_{_r},\boldsymbol{j}_{_0} \right)& \cos \left( \boldsymbol{k}_{_r},\boldsymbol{j}_{_0} \right)\\ \cos \left( \boldsymbol{i}_{_r},\boldsymbol{k}_{_0} \right)& \cos \left( \boldsymbol{j}_{_r},\boldsymbol{k}_{_0} \right)& \cos \left( \boldsymbol{k}_{_r},\boldsymbol{k}_{_0} \right)\\ \end{matrix} \right] \left[ \begin{array}{c} R_{x}^{r}\\ R_{y}^{r}\\ R_{z}^{r}\\ \end{array} \right]\] \[\left[ \begin{array}{c} R_{x}^{r}\\ R_{y}^{r}\\ R_{z}^{r}\\ \end{array} \right] =\left[ \begin{matrix} \cos\mathrm{(}\boldsymbol{i}_r,\boldsymbol{i}_0)& \cos\mathrm{(}\boldsymbol{i}_r,\boldsymbol{j}_0)& \cos\mathrm{(}\boldsymbol{i}_r,\boldsymbol{k}_0)\\ \cos\mathrm{(}\boldsymbol{j}_r,\boldsymbol{i}_0)& \cos\mathrm{(}\boldsymbol{j}_r,\boldsymbol{j}_0)& \cos\mathrm{(}\boldsymbol{j}_r,\boldsymbol{k}_0)\\ \cos\mathrm{(}\boldsymbol{k}_r,\boldsymbol{i}_0)& \cos\mathrm{(}\boldsymbol{k}_r,\boldsymbol{j}_0)& \cos\mathrm{(}\boldsymbol{k}_r,\boldsymbol{k}_0)\\ \end{matrix} \right] \left[ \begin{array}{c} R_{x}^{0}\\ R_{y}^{0}\\ R_{z}^{0}\\ \end{array} \right]\]
   • 上述九个方向余弦可以组成方向余弦矩阵
   • 对于刚体坐标系的一个角位置，就有唯一的一组方向余弦与其对应
   • 方向余弦矩阵可以确定定点转动刚体在空间的角位置，其中 $C_{r}^{0}$ 是第一个， $r \rightarrow 0$ 称为 $r$ 对 0 系的方向余弦矩阵，$C_{0}^{r}$ 是第二个，$0\rightarrow r$ ，称为0系对 $r$ 系的方向余弦矩阵。

3. 两个方向余弦矩阵的性质

   

欧拉角法

1. 定义

   刚体坐标系相对参考坐标系的角位置，可以使用三次独立的三个转角来确定，这就是欧拉角法原理

2. 欧拉角的选取并不是唯一的

   • 第一次转动可以是刚体坐标系的任意一根轴
   • 第二次转动是其余两根 二选一
   • 第三次转动是在除了第二次转动的那一根外二选一即可

3. 欧拉角法和方向余弦法之间的联系

   假设第一次绕着 $x_0$ 轴转 $\alpha$ 角，第二次绕 $y_0$ 转 $\beta$ 角，第三次绕 $z_0$ 转 $\gamma$ 角。

   将各个坐标系分别记为 0 系、a 系、b系和 r系。

   \[C_{0}^{a}=\left[ \begin{matrix} 1& 0& 0\\ 0& \cos \alpha& \sin \alpha\\ 0& -\sin \alpha& \cos \alpha\\ \end{matrix} \right]\] \[C_{a}^{b}=\left[ \begin{matrix} \cos {\beta }& 0& -\sin {\beta }\\ 0& 1& 0\\ \sin {\beta }& 0& \cos {\beta }\\ \end{matrix} \right]\] \[C_{b}^{r}=\left[ \begin{matrix} \cos \gamma& \sin \gamma& 0\\ -\sin \gamma& \cos \gamma& 0\\ 0& 0& 1\\ \end{matrix} \right]\] \[C_{0}^{r}=C_{b}^{r}C_{a}^{b}C_{0}^{a}=\\ \left[ \begin{matrix} \cos \beta \cos \gamma& \sin \alpha \sin {\beta}\cos \gamma +\cos \alpha \sin \gamma& -\cos \alpha \sin {\beta}\cos \gamma +\sin \alpha \sin \gamma\\ -\cos \beta \sin \gamma& -\sin \alpha \sin {\beta}\sin \gamma +\cos \alpha \cos \gamma& \cos \alpha \sin{\beta}\sin \gamma +\sin \alpha \cos \gamma\\ \sin {\beta}& -\sin \alpha \cos \beta& \cos \alpha \cos \beta\\ \end{matrix} \right]\]
   • 一组欧拉角可以唯一确定九个方向余弦
   • 一组方向余弦也可以唯一确定三个欧拉角
   \[\begin{aligned} &\alpha= \arctan(-T_{32}/T_{33})\\ &\beta=\arcsin(T_{31})\\ &\gamma=\arctan(-T_{21}/T_{11}) \end{aligned}\]