#惯性导航# 4. 平台式惯性导航系统
平台式惯性导航系统
1. 惯导系统基本概念
- 惯导系统的优越性:
- 自主性
- 信息的全面性
- 数据更新率高
- 短期精度高
- 稳定性好
- 惯性导航系统工程实现需要解决的关键问题
- 必须采用一组高精度的加速度计作为测量元件
- 需要一组高性能的陀螺仪来模拟一个稳定的导航坐标系
- 必须有效地将运动加速度和重力加速度分离开,并补偿其他不需要的加速度分量
- 必须建立全面的计算和补偿网络,采用的计算装备要有足够的计算精度和运算速度
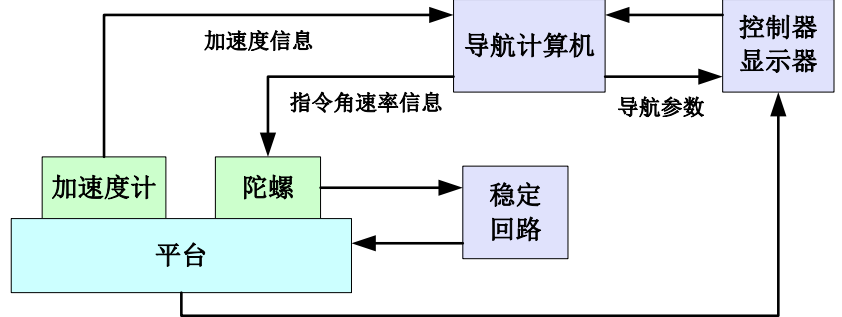
惯导系统的组成:
- 测量惯性组件
- 加速度计
- 陀螺仪
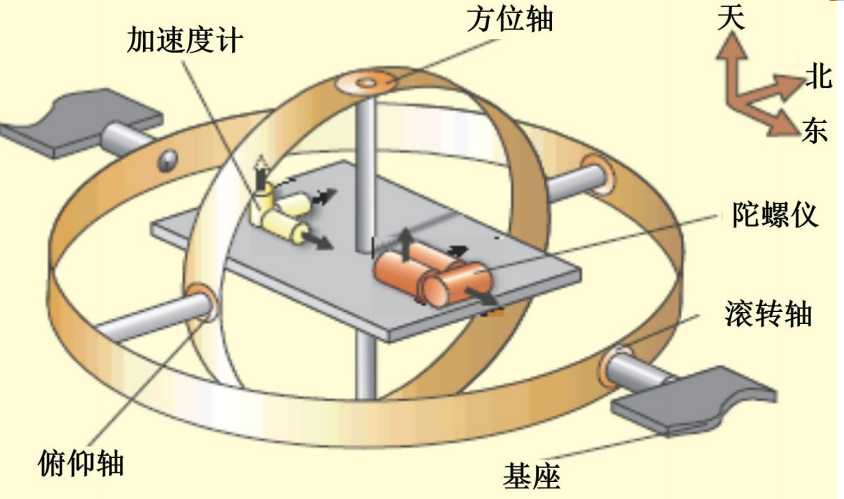
- 惯导平台
- 专用计算机
- 控制显示器
- 测量惯性组件
惯导系统的分类
根据惯性测量装置在载体上的安装方式,可以分为:平台式惯性导航系统&捷联式惯性导航系统
2. 平台式惯导系统信息
作为惯导系统要解决的问题有以下几个方面:
- 如何由比力信息中提取所需的加速度信息
- 如何进行平台指令角速率及导航参数的计算
- 如何使用平台回路满足舒勒调谐
- 如何进行精确的初始对准
比力方程和加速度信息提取
若选取平台坐标系作为测量坐标系,比力定义式可以分解为:
\[f=\dot{v}_{ep}+(2\omega_{ie}+\omega_{ep})\times v_{ep}-g\]$\dot{v_{ep}}$ 是平台相对地球坐标系的加速度,是惯导系统要提取的信息 $2\omega_{ie} \times v_{ep}$ 是载体的相对速度 $v_{ep}$ 与牵连角速度 $\omega_{ie}$ 引起的哥氏加速度 $\omega_{ep}\times v_{ep}$ 是测量坐标系相对地球转动引起的向心加速度 $g$ 是当地重力加速度,其中 $g=G-\omega_{ie}\times (\omega_{ie}\times r )$ ,地球的引力加速度和地球自转的向心加速度之差构成了地球重力加速度
\[\dot{v_{ep}}=f-[(2\omega_{ie}+\omega_{ep})\times v_{ep}-g]=f-a_B\]必须从测得的比力中补偿掉有害加速度$a_B$,才能提取出测量平台运动加速度 $\dot{v_{ep}}$
如果平台精确跟踪一个当地水平坐标系,则有: \(g^p=\left[ \begin{array}{c} g_x\\ g_y\\ g_z\\ \end{array} \right] =\left[ \begin{array}{c} 0\\ 0\\ g\\ \end{array} \right]\)
惯性平台的运动
- 平动:由平台稳定回路实现
- 转动:由平台修正回路实现
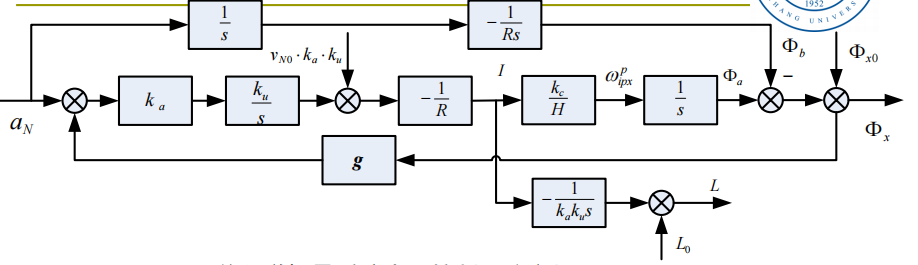
平台水平控制回路及舒勒调谐
当输入$\Phi_{x0}=0$ ,即初始对准后,现在需要使得输出的$\Phi_x$ 平衡处始终为0。其实就是进行所谓的舒勒调谐:
只需要使得两个前向回路的作用相互抵消,反馈回路就不起作用:
\[\frac{k_ak_uk_c}{RHs^2}=\frac{1}{Rs^2}\]此时可以可得系统微分方程:
\[\ddot{\Phi}_x+\frac{g}{R}\Phi _x=0\]此时系统固有频率:
\[\omega_s=\sqrt{g/R}\]相应的$T=84.4 \textbf{min}$
因此,
\[\frac{k_ak_uk_c}{H}=1\]就是平台水平控制回路的舒勒调谐条件。
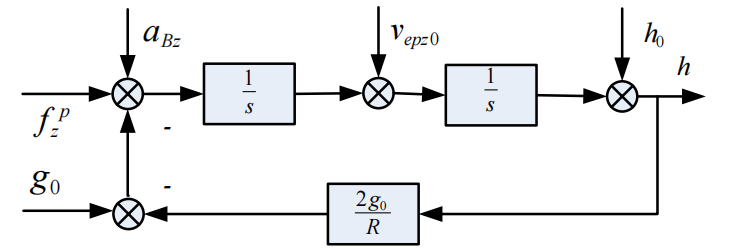
惯导系统高度通道的问题
由比力方程,可以得到标量式:
\[\dot{v}_{epz}^p=f_z^p+a_{Bz}-g\]其中,当$h«R$时,
\[g=K\frac{Mm}{(R+h)^2}\approx g_0(1-\frac{2h}{R})\]- 系统特征方程有一个正根,说明系统是不稳定的发散系统,计算高度的误差是扩散型的。
- 因此,不能直接采用纯惯性的高度通道,必须引入外部高度信息进行组合,使得系统获得必要的阻尼后再求高度。
3. 惯导系统组成部分
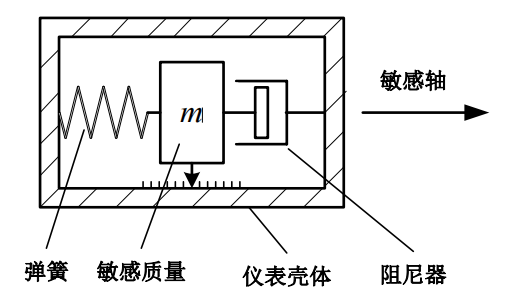
加速度计
- 又称比力敏感器——以牛顿惯性定律作为理论基础
注意,其中 $x$ 是形变量。
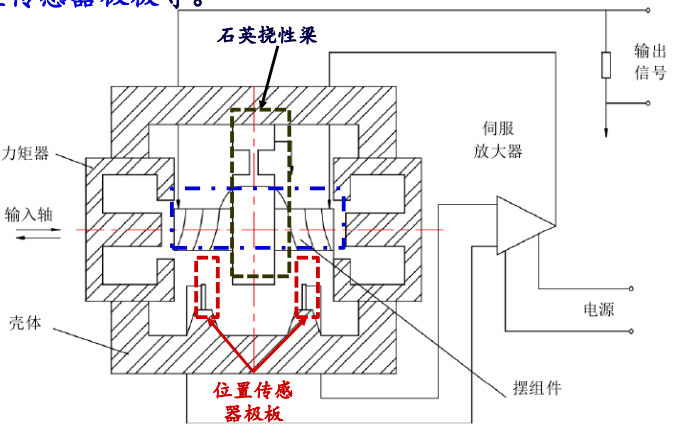
石英挠性加速度计
主要组成结构:
- 摆组件(由线圈和石英摆片组成)
- 石英挠性梁
- 位置传感器极板
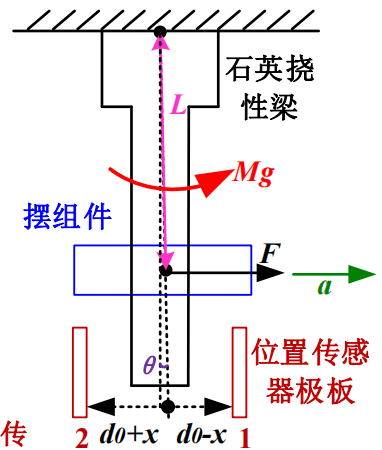
其实就是通过双边电容之差(差动电容)产生电流信号$I$,反馈给力矩器线圈,产生与加速度方向相反的电磁力,进而产生电磁反馈力矩$M_t$
- 当加速度力矩与电磁力矩相反,大小相等时,即平衡。
- \[M_t=K_tI\\ M_g=FL=maL\\ M_t=M_g\]
可得,$I=\frac{mL}{K_t}a$ ,因此,只需检测出力矩器线圈中电流的大小,便可以测量的得到实际加速度的大小。
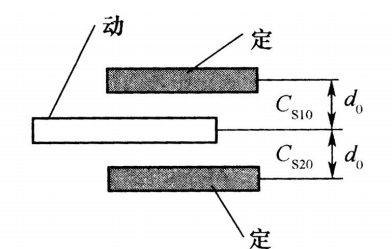
微机电加速度计
当有加速度$a$ 输入时,差动电容:
\[\Delta C=\frac{2C_{S0}}{d_0}x\]此外,由材料力学知识可知,动片受力与位移满足
\[K_mx=ma\]联立两式,得
\[\Delta C=\frac{2mC_S0}{K_md_0}a\]差动电容与$a$ 成正比。只需要测量出这个微小电容量的变化,即可得知输入加速度的大小。
寻北仪
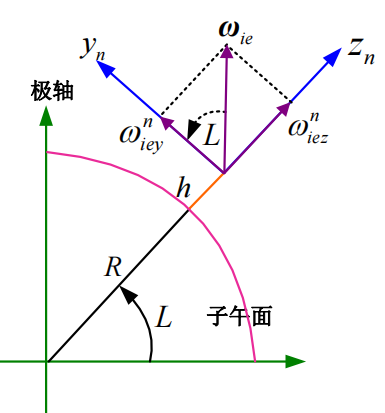
地球自转角度度在子午面的投影与分解关系如图所示:
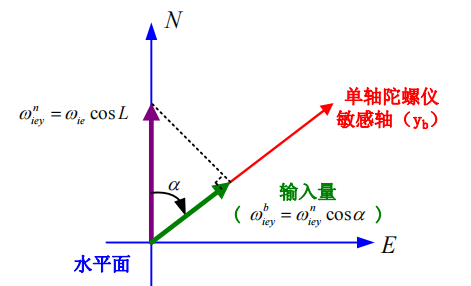
\[\begin{cases} \omega _{iex}^{n}=0\\ \omega _{iey}^{n}=\omega _{ie}\cos L\\ \omega _{iez}^{n}=\omega _{ie}\sin L\\ \end{cases}\]而地球自转角速度在水平面内投影与分解关系如下图所示:
若一个单轴速率陀螺的敏感轴在水平面内,显然当陀螺输出值最大时,其敏感轴指向就是真北方位——这就是陀螺寻北仪的原理。
- 寻北过程无需外部参考,不受天气、昼夜时间、地磁场等条件的影响。
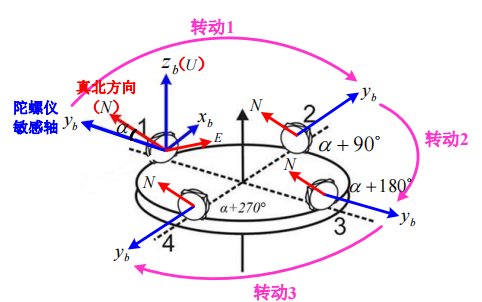
$y$ 轴方向的投影量为 $\omega_{ie}\cos L\cos \alpha +\varepsilon (t_1)$
随后,转动基座90度,测量轴向角速度,重复三次,直到陀螺返回原位。
短时间内,假设陀螺漂移量为一个常量,则有
\[\begin{cases} \omega _{_1}=\omega _{_{ie}}\cos L\cos \alpha +\varepsilon\\ \omega _{_2}=-\omega _{_{ie}}\cos L\sin \alpha +\varepsilon\\ \omega _{_3}=-\omega _{_{ie}}\cos L\cos \alpha +\varepsilon\\ \omega _{_4}=\omega _{_{ie}}\cos L\sin \alpha +\varepsilon\\ \end{cases}\]可以计算出陀螺仪敏感轴与真北方向的夹角:
\[\alpha=\arctan(\frac{\omega_4-\omega_2}{\omega_1-\omega_3})\]用此方法测量,可以消除陀螺的零偏,也无需知道测量地点的纬度值。
若测量地点纬度 $L$ 已知,那么只需测量1和3(或者2和4)两个位置即可求出航向角。
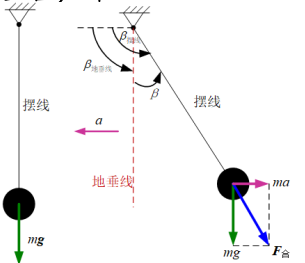
地平仪
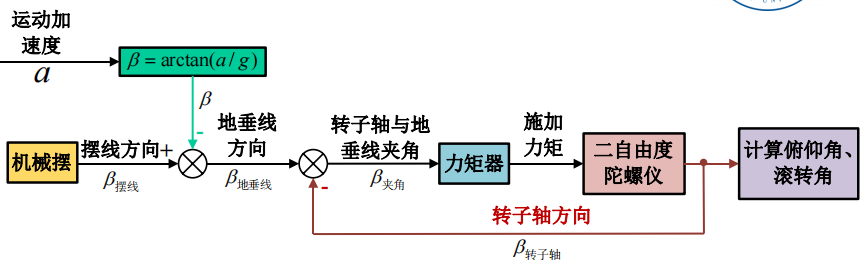
地平仪式利用机械摆能够敏感地垂线方向的特性,并结合二自由度陀螺仪的定轴性和进动性研制而成的。
核心公式就在于保证下式恒成立,其中$\beta=\arctan(a/g)$:
\[\beta_{夹角}=(\beta_{摆线}-\beta)-\beta_{转子轴}=\beta_{地垂线}-\beta_{转子轴}=0\]将$\beta_{夹角}$ 作为力矩器的输入信号,力矩器对陀螺仪施加力矩使其进动,保持陀螺转子轴与地垂线重合。
地平仪测量水平姿态角原理
现在已经通过机械摆和二自由度陀螺仪的结合能够在运动的载体上建立一个稳定的垂线基准。现在需要利用这一垂线基准进一步获得载体的水平姿态角。
按照$z$ 轴偏航 $(\psi)$ ,绕$x$ 轴俯仰 $(\theta)$ ,绕$y$ 轴滚转 $(\gamma)$ 的转序定义飞机姿态,则飞机本体系b相对导航系n系的坐标转换矩阵为:
\[C_n^b=L_y(\gamma)L_x(\theta)L_z(\psi)\\ =\begin{bmatrix} \cos(\gamma)\cos(\psi) + \sin(\gamma)\sin(\theta)\sin(\psi) & -\cos(\gamma)\sin(\psi) + \sin(\gamma)\sin(\theta)\cos(\psi) & -\sin(\gamma)\cos(\theta) \\ \sin(\psi)\cos(\theta) & \cos(\psi)\cos(\theta) & \sin(\theta) \\ \sin(\gamma)\cos(\psi) - \cos(\gamma)\sin(\theta)\sin(\psi) & -\sin(\gamma)\sin(\psi) - \cos(\gamma)\sin(\theta)\cos(\psi) & \cos(\gamma)\cos(\theta) \end{bmatrix}\]由此可得重力在b系下表示为:
\[g^b=C_n^bg_n=[g\sin\gamma \cos\theta,-g\sin\theta,-g\cos\theta]^{\textbf{T}}\]由上式求得俯仰角和滚转角:
\[\theta=\arcsin(-g_y^b/g)\\ \gamma=\arctan(-g_x^b/g_z^b)\]4. 指北方位管惯导系统
平台指令角速度
- 指北方位惯导系统选择当地地理坐标系$t$ 作为导航坐标系。Thus,平台坐标系$p$ 在工作中将始终跟踪地理坐标系$t$。
- 这样,按照 $\omega_{ip}^p$ 的三个分量计算形成的电信号分别送给平台上相应的陀螺力矩器,既可以实现$p$ 系对 $t$ 系的追踪。
速度计算
由于指北方位惯导系统的$p$ 系与 $t$ 系保持一致,则:
\[\dot{\boldsymbol{v}}_{et}^{t}=\boldsymbol{f}^t-\left( 2\boldsymbol{\omega _{ie}^{t}}+\boldsymbol{\omega _{et}^{t}} \right) \times \boldsymbol{v}_{et}^{t}+\boldsymbol{g}^t\]将$\omega_{ie}^t$和$\omega_{et}^t$代入上式:
\[\begin{cases} \dot{v}_{x}^{t}=f_{x}^{t}+\left( 2\omega _{ie}\sin L+\frac{v_{x}^{t}}{R_{xt}}\tan L \right) v_{y}^{t}-\left( 2\omega _{ie}\cos L+\frac{v_{x}^{t}}{R_{xt}} \right) v_{z}^{t}\\ \dot{v}_{y}^{t}=f_{y}^{t}-\left( 2\omega _{ie}\sin L+\frac{v_{x}^{t}}{R_{xt}}\tan L \right) v_{x}^{t}-\frac{v_{y}^{t}}{R_{yt}}v_{z}^{t}\\ \dot{v}_{z}^{t}=f_{z}^{t}+\left( 2\omega _{ie}\sin L+\frac{v_{x}^{t}}{R_{xt}} \right) v_{x}^{t}+\frac{v_{y}^{t}}{R_{yt}}v_{y}^{t}-g\\ \end{cases}\]\[\begin{cases} \dot{v}_{x}^{t}={f}_{x}^{t}+2\omega _{_{ie}}\sin L\cdot {v}_{y}^{t}+\frac{v_{x}^{t}{v}_{y}^{t}}{R_{_{xt}}}\tan L\\ \dot{v}_{y}^{t}={f}_{y}^{t}-2\omega _{_{ie}}\sin L\cdot {v}_{x}^{t}-\frac{\left( {v}_{x}^{t} \right) ^2}{R_{_{xt}}}\tan L\\ \end{cases}\]对于飞机和舰船来说,$v_z^t$ 比 $v_x^t,v_y^t$ 小很多,可以作为小量略去,高度通道另行计算
根据上式从加速度计测得的比力中消去有害加速度,积分即可得当地水平面速度:
\[v=\sqrt{(v_x^t)^2+(v_y^t)^2}\]纬度、经度计算
\[\begin{cases} \dot{L}=\frac{v_{y}^{t}}{R_{yt}}=-\omega _{etx}^{t}\\ \dot{\lambda}=\frac{v_{x}^{t}}{R_{xt}\cos L}=\frac{\omega _{etz}^{t}}{\sin L}\,\,\left( \omega _{etz}^{t}=\dot{\lambda}\sin L=\frac{v_E}{R_{xt}}\tan L \right)\\ \end{cases}\]Thus,由$v_x^t,v_y^t$ 积分即可求出纬度$L$ 与经度 $\lambda$
高度计算
纯惯性的高度通道是不稳定的,必须引入外部的高度信号(气压高度表、无线电高度表、大气数据系统等)来对高度通道构成阻尼回路,这样可以得到动态品质较好而误差又不随时间发散的组合高度系统。
姿态角的获取
- 由于指北方位平台坐标系直接模拟了当地地理坐标系,所以可以从平台框架轴上的角度传感器(同步器)直接获得载体的姿态角
- 加速度计输出的比力信号不用经过其它坐标变换,便直接求得所需的导航参数。
- 系统的计算工作量较小
- 对计算机要求不很高,易于实现
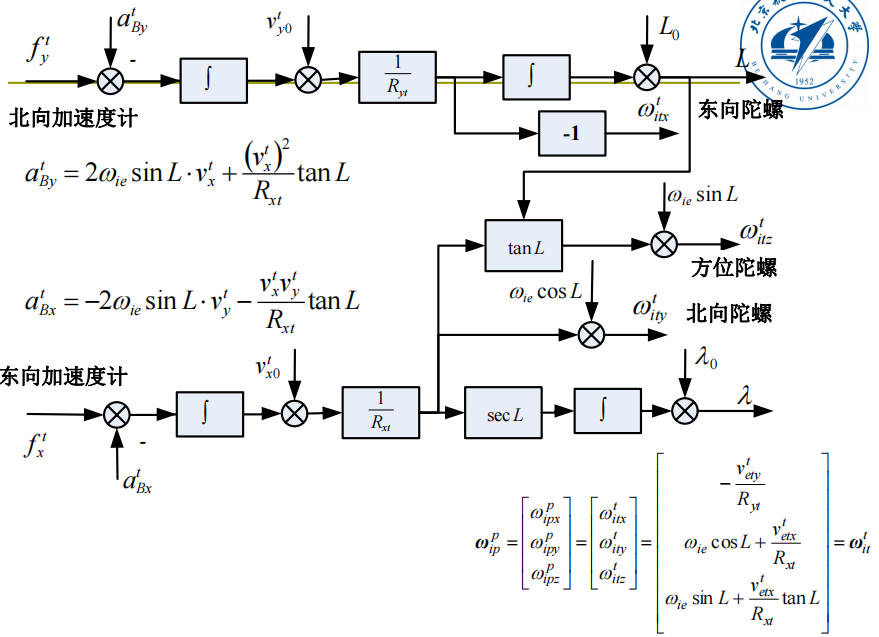
指北方位惯导系统原理图
优势与问题
优点
- 平台坐标系跟踪地理坐标系
- 加速度计输出的比力信号不用经过其他坐标变换就可求得所需导航参数
- 姿态角可以从平台框架是哪个直接取得
- 计算过程中所用的地球曲率半径是主曲率半径,计算量比较小
- 系统计算比较简单,对计算机要求不高,易于实现
问题
\[\omega_{itz}^t=\omega _{ie}\sin L+\frac{v_{etx}^{t}}{R_{xt}}\tan L\]- 当载体在$L=70°\sim90°$ 区域飞行时,指令角速度随着纬度的增加而急剧增大,要求陀螺力矩器接受很大的指令电流,平台也要以高角速度绕$OZ_p$ 轴转动,因此给稳定回路的设计造成很大困难
- 载体在极区飞行有可能使计算机在计算 $\tan L$ 时发生溢出
因此,指北方位系统不能满足全球导航的需要!
5. 自由方位惯导系统
平台轴 $y_p$ 不跟踪地理北向而是与地理北向夹某个角度,称自由方位角。
- 根据方位角的变化规律,又分为自由方位、游动方位。
- 自由方位惯性系统采用的导航坐标系仍为一个水平坐标系,$OX_p$ 与 $OY_p$ 始终处于当地水平面内,但在方位上相对惯性空间保持稳定。
而$p$ 系与 $t$ 系的$Z$ 轴重合,则$\omega_{ipz}^t=\omega_{ipz}^p$ ,又
\[\omega_{ipz}^t=\omega_{itz}^t+\omega_{tpz}^t=0\]则有:
\[\omega_{ipz}^t=-\omega_{itz}^t=-(\omega_{ie}\sin L+\frac{v_{etx}^{t}}{R_{xt}}\tan L)\]这实际上就是平台绕着$z$ 轴相对地理系的表观运动的相反数。
显然,由于自由方位系统的$\omega_{ipz}^p=0$,陀螺$G_z$ 不需施加力矩,因此可以避免在前文指北方位系统在高纬度地区飞行时遇到的问题。
6. 游动方位惯导系统
- 游动方位惯导系统的平台坐标系仍为当地水平坐标系
- 但与自由方位系统的区别:对方位陀螺力矩器上施加有限的指令角速率
- 平台绕$OZ_p$ 轴只跟踪地球本身的转动,而不跟踪由载体地速引起的当地地理系的转动
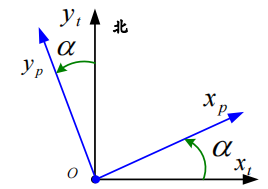
设$OY_p$ 轴与地理系$OY_t$轴之间的夹角为$\alpha$ ——游动方位角
\[\omega_{tpz}^p=\omega_{ipz}^p-\omega_{itz}^p=\dot{\alpha}=-\frac{v_{etx}^{t}}{R_{xt}}\tan L\]游动方位系统虽然在$G_z$上有指令信号,但由于$\omega_{ipz}^p$ 很小,因此不会发生指北方位系统在高纬度地区航行出现的问题
而在利用方向余弦矩阵解算导航参数时,该方案比自由方位系统简单,计算量小,Thus,现行惯导系统大部分采用游动方位的方案。