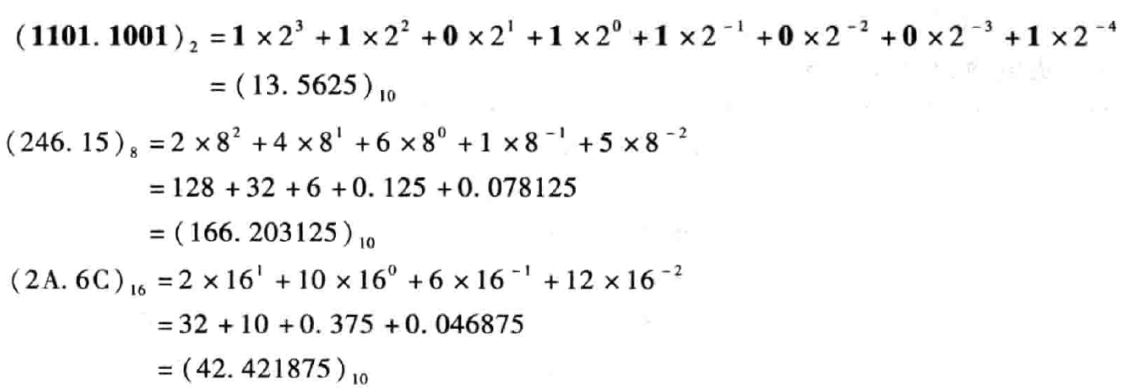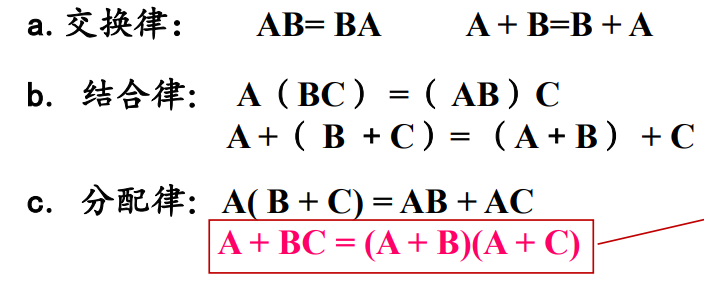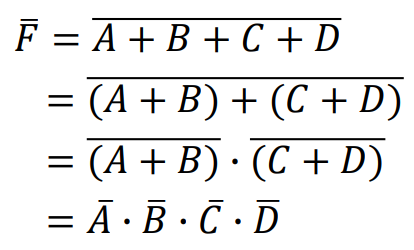Post

Information & Logic

Posted Updated
By Young Friday
6 min read
Information & Logic

Information & Logic

1. 信息 Information

Information resolves uncertainty. –Claude Shannon

$N$个选择，若有一事实可以将其缩小至$M$个选择，则此事件信息量为： \(\log _2\frac{N}{M} \text{bits of information}\)

1.1 信息的编码

编码是对信息进行表征的过程

编码方式会直接影响

  • Mechanism
  • Efficiency
  • Reliability
  • Security

1.2 数制与码制

  • 表示数量时，可以比较大小，表示代码时，不可以比较大小
  • 数制：表示数量的规则（对数进行编码）
  • 码制：表示事物的规则（对事物进行编码）

1.2.1 常用数制

进位计数值

  1. 二进制、八进制、十六进制 $\Rightarrow$ 十进制

image-20240909210724542

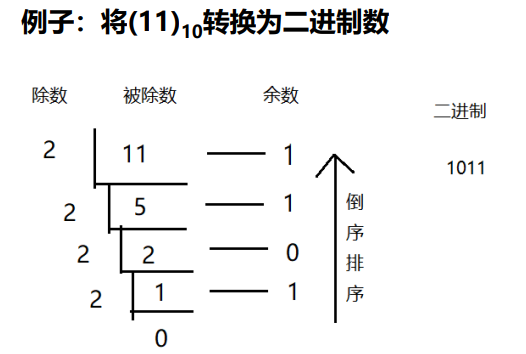
  1. 十进制 $\Rightarrow$ 二进制

    • 整数转换：整数连除，取余逆序

      image-20240909211209100

    • 纯小数的转换：小数连乘，取整顺序

      image-20240909211226061

  2. 十进制$\Rightarrow$ 八进制、十六进制转换（同上）

    image-20240909211900636

  3. 二进制 $\Rightarrow$ 八进制

    image-20240909212145733

  4. 八进制 $\Rightarrow$ 二进制

    image-20240909212240075

  5. 二进制$\Leftrightarrow$ 十六进制

    image-20240909212428505

  6. 八进制$\Leftrightarrow$ 十六进制

    以二进制为中介，先转换为二进制数，再转换为对应的进制数

1.2.2 二进制数的运算

  1. 无符号数

    image-20240909213320126

  2. 带符号数

    定点运算中，最高为为符号位（0为正，1为负）

  3. 源码、反码、补码

    • 原码：符号位+数值位 \((+5)_{10}=(00101)_{原码}\\ (-5)_{10}=(10101)_{原码}\)

    • 反码：正数的反码为其本身，负数的反码数值位逐位取反 \((+5)_{10}=(00101)_{反码}\\ (-5)_{10}=(11010)_{反码}\)

    • 补码：正数的补码为其本身，负数的补码为其反码的数值位加1

      对于为什么要加1，可以参考知乎文章：其实源于二进制的范围是$0\sim2^{n-1}$，比如8位是11111111=255，比256少1，所以需要补上1.

      为什么补码要加一？

      \((+5)_{10}=(00101)_{反码}=(00101)_{补码}\\ (-5)_{10}=(11010)_{反码}=(11011)_{补码}\) 计算机中二进制的运算常常使用补码系统

image-20240909220858776

1.2.2 常用码制

  1. BCD码
    • 并不是二进制数
    • 最常用的是格雷码，顺序变化时，相邻代码只有一位改变状态
  2. ASCII码
    • 使用7位二进制数

逻辑运算

image-20241229114903432

逻辑代数基础

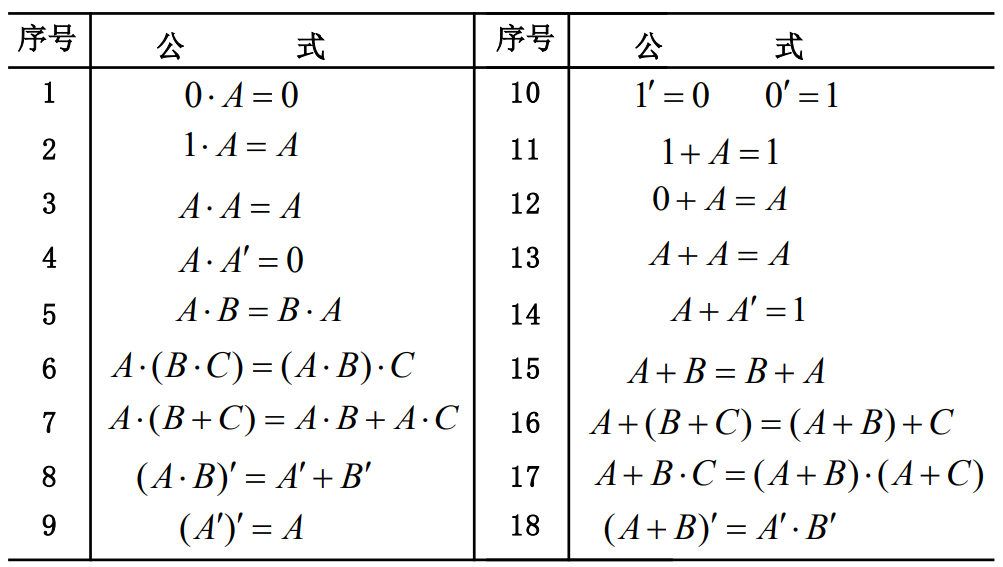
1.布尔代数基本公式

image-20240909222137829

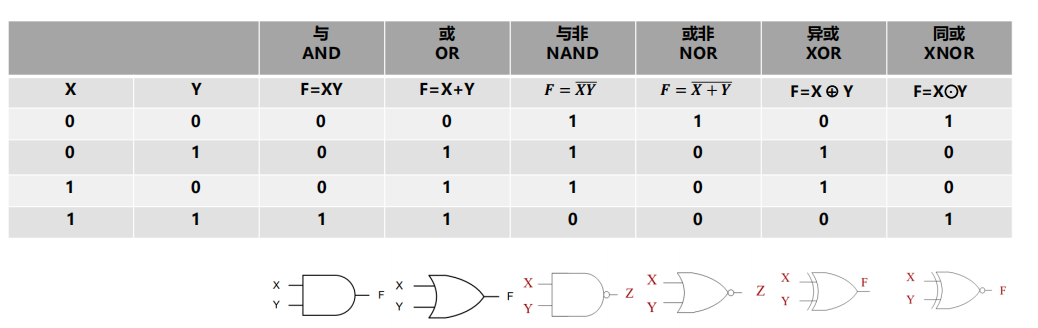
2. 基本逻辑关系

image-20240909222429455

3. 逻辑函数的化简公式

image-20240909223235486

摩根定律：

\[\overline{A\cdot B}=\overline{A}+\overline{B}\] \[\overline{A+B}=\overline{A}\cdot \overline{B}\]

image-20240909223743303

4.逻辑运算的优先级别

  1. 括号 长非号
  2. 与
  3. 异或 同或
  4. 或

5. 逻辑函数的5类基本形式

  • 与或 $AB+BC$
  • 与非-与非(与非式) $\overline{AB}\cdot\overline{AC}$ Q:$\overline{AB}+\overline{AC}$ ?
  • 与或非 $\overline{AB+AC}$
  • 或与 $(A+B)(A+C)$
  • 或非-或非（或非式） $\overline{A+B}+\overline{A+C}$

逻辑函数的表示与化简

1.表示方法

  • 表达式
  • 真值表
  • 卡诺图
  • 逻辑电路图
  • 波形图

2.最小项 、标准与或式 、 最大项

2.1 最小项

  • 每个与项均包含了该逻辑函数的所有变脸，每个变量只能以原变量或者反变量的形式出现一次
  • n变量逻辑函数共有$2^n$个最小项
  • 在输入变量的任一组取值下，有且仅有一个最小项的值为1
  • 一个逻辑函数的任意两个最小项之积必为0
  • 一个逻辑函数的全体最小项之和必为1

2.2 标准与或式

  • 由最小项相加得到的与或表达式，又称最小项标准式
  • 唯一性

2.3 最大项

  • 或项
  • 包含全部变量
  • 每个变量以原变量或者反变量的形式只出现一次 $A+B+C$ 、 $A+B+\overline{C}$

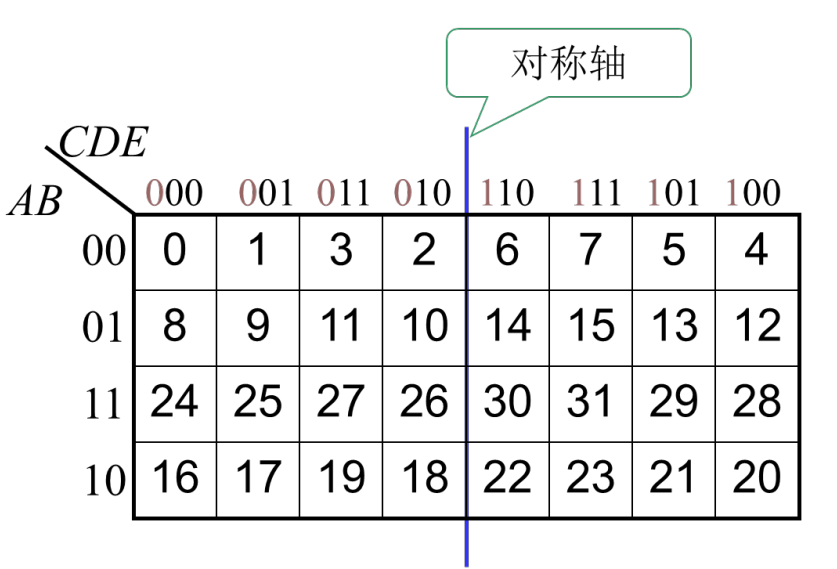
3.卡诺图

将逻辑函数真值表中的最小项重新排列成矩阵形式，并且使矩阵的横方向和纵方向的逻辑变量的取值按照格雷码的顺序排列，这样构成的图形就是卡诺图

  • n≥5 变量的卡诺图，可由n－1变量卡诺图在需要增加变量的方向采用镜像变换而生成

    image-20240909235002688

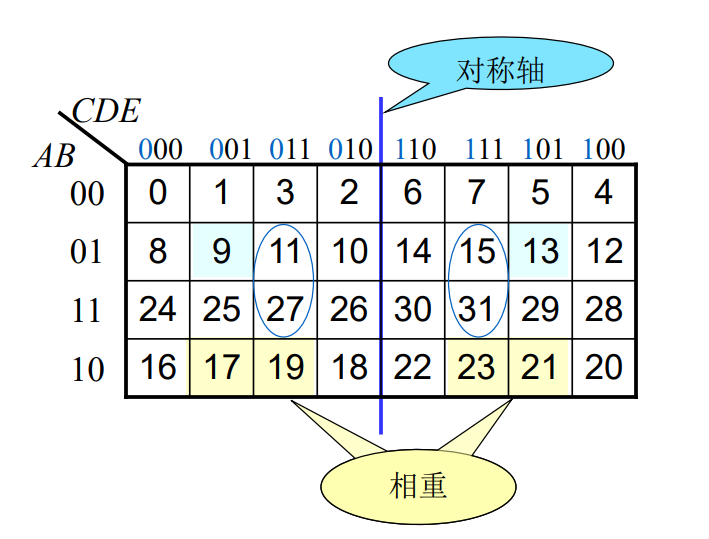
3.1 逻辑相邻项

指两个最小项,只有一个变量的形式不同,其余的都相同,并且逻辑相邻的最小项可以合并

具有逻辑相邻性的方格有：

  • 相接——几何相邻的方格

  • 相对——上下两边、左右两边的方格

  • 相重——多变量卡诺图，以对称轴相折叠，重在一齐的方格

    image-20240909235750796

3.2 画圈原则

  1. 方格数是$2^i$个
  2. 圈要尽量大
  3. 每个圈都要有新的方格
  4. 不能漏掉任何一个标1的方格
NOTES, VLSI
Information
This post is licensed under CC BY 4.0 by the author.