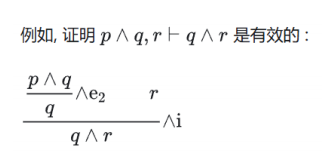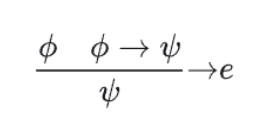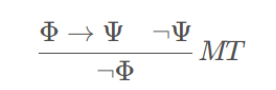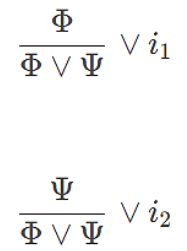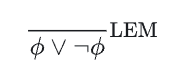Knowledge Graph

Knowledge Graph

知识推理

在已有知识的基础之上，推断出位置的知识的过程。

• 基于本体公理的推理
• 基于图结构的推理
• 基于表示学习的推理
• 基于逻辑结构的推理
• 基于神经网络的推理
• 混合推理

基于规则的推理

应用：基于不完备知识库的关联规则挖掘算法 AMIE

Association Rule Mining under Incomplete Evidence

自然演绎

\[\boldsymbol{\phi }_{\boldsymbol{1}},\boldsymbol{\phi }_{\boldsymbol{2}},\boldsymbol{\phi }_{\boldsymbol{3}},...,\boldsymbol{\phi }_{\boldsymbol{n}}\vdash \boldsymbol{\psi }\]

• 上式为相继式(sequent)，如果我们可以建立证明，则称它为有效(valid)
• $\vdash$ 是句法后承(syntactic consequence)关系
• 读作 ：$\boldsymbol{\psi }$ 可以证明自 $\boldsymbol{\phi }{\boldsymbol{1}},\boldsymbol{\phi }{\boldsymbol{2}},\boldsymbol{\phi }{\boldsymbol{3}},…,\boldsymbol{\phi }{\boldsymbol{n}}$

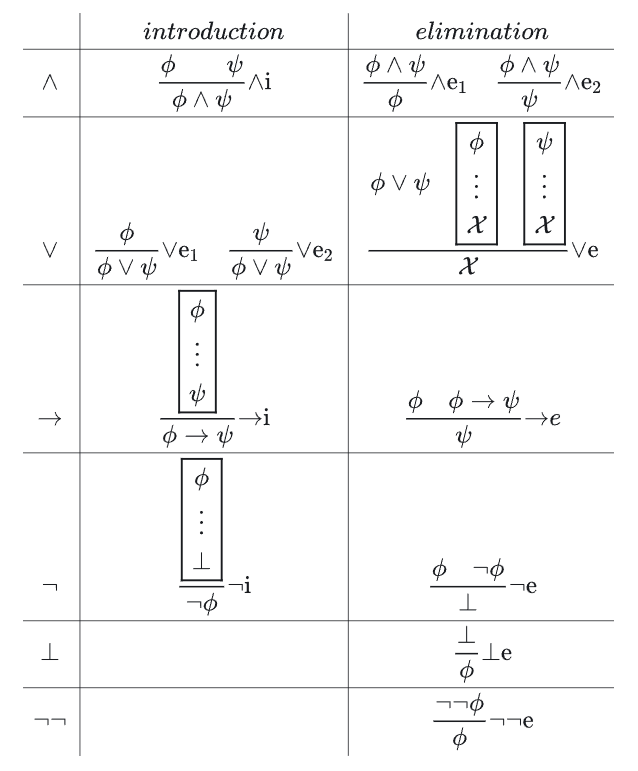
自然演绎规则

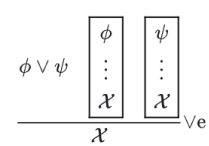
• 合取规则 （合取相当于 “且”，合就是二者都成立）

• 双重否定规则

• 蕴含消去规则/分离规则

• 蕴含消去规则/反证规则

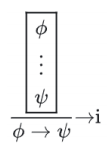
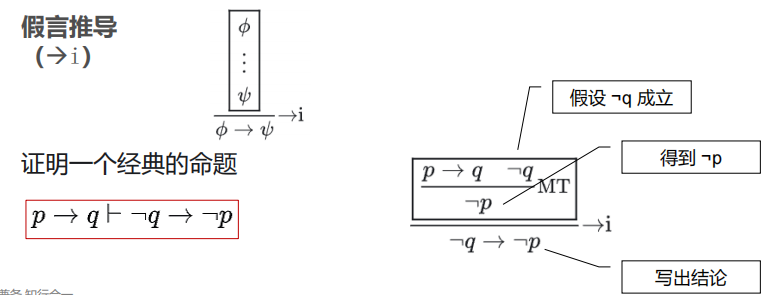
• 蕴含引入规则/假言推导

方框代表在框内做假设：我们为了证明 $\phi \rightarrow \psi$ ，先假设 $\phi$ 成立，再证明 $\psi$ ，假设在框外不成立。

很好理解，你想证明一个带 $\rightarrow$ 的式子成立，并且 $\rightarrow$ 左侧的东西还不是前提，总得假设一下吧哈哈哈

• 析取规则 （“析取”相当于“或”，析就是分开成立即可）

  1. 析取引入规则：

     

  2. 析取消除规则：

     

• 否定规则 (($\bot$ 矛盾)

不要试图去理解矛盾律 知乎回答

反证法的运用 (proof by contradiction ,PBC)

• 排中律

对于任何 $\phi$，有 $\boldsymbol{\phi }\land \lnot \boldsymbol{\phi }$ 为真

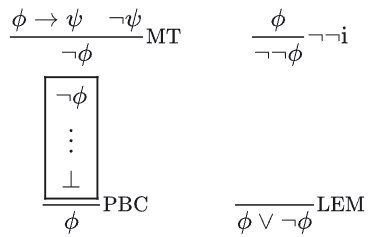
总结

以及一些衍生规则：

基于表示学习的推理

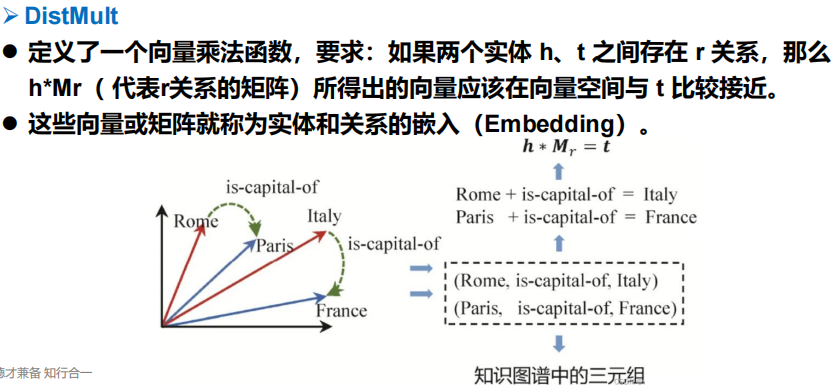
深度学习和表示学习的兴起启发了人们研究基于向量表示的推理方法。例如，TransE 和 DistMul 等知识图谱嵌入系列模型。

• DisMult

• TransE