Logic Gate Circuit (CMOS & TTL)
Logic Gate Circuit (CMOS & TTL)
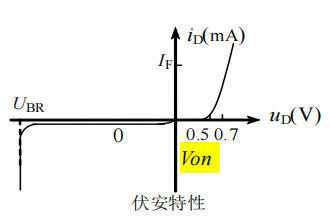
1. Diode
Properties
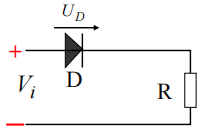
开关作用
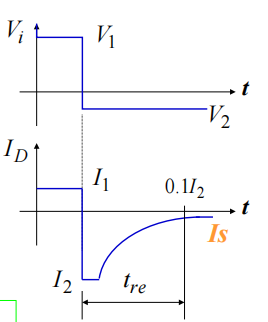
动态特性
门电路
- 优点:结构简单
- 缺点:不实用,如电平偏移、带负载能力差
2. CMOS
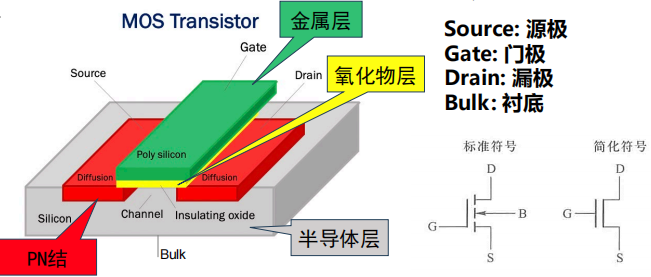
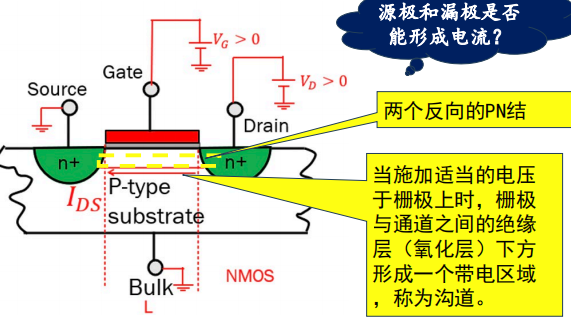
2.1 The structure of MOS
一般情况下:
源极(S)与衬底(B)是短接的(图中是一并接地的)
在简写符号中,箭头$\rightarrow$的方向就是$P\rightarrow N$的方向(中间那个小块是衬底B!!!)
在$GB$ or $GS$之间加电压即可使得$SD$之间导通
- PMOS: $V_{GB}<0$,氧化层下方形成“+”沟道(少数载流子空穴聚集)
- NMOS: $V_{GB}>0$,氧化层下方形成“-”沟道(少数载流子电子聚集)
2.2 Input & Output of MOS
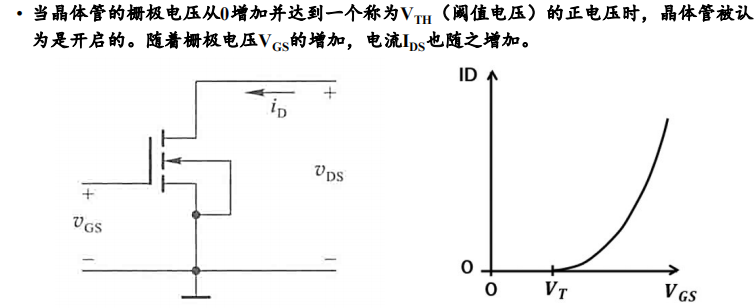
When $V_{DS}=\text{const}$
原因在于$V_{GS}++$,导电沟槽的截面积++,$I_{DS}++$
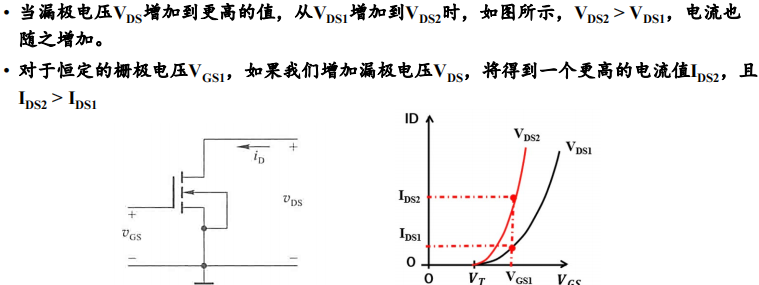
When $V_{DS}\ne\text{const}$
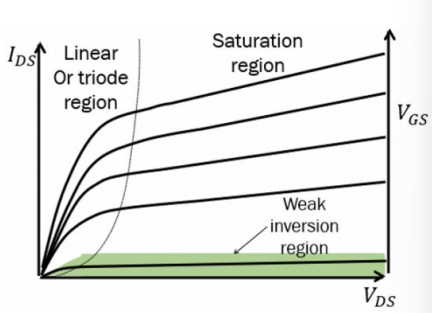
When $V_{DS}\ V_{GS} $ changing together
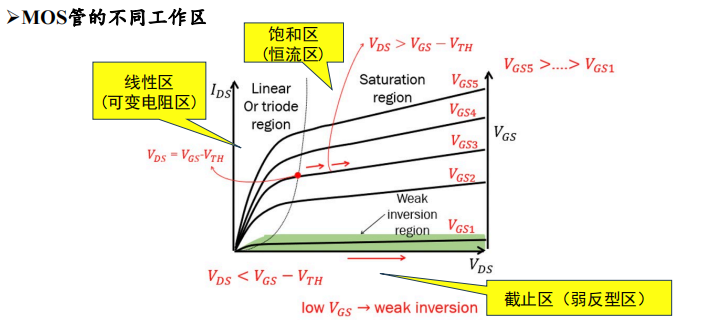
MOS 管的不同工作区
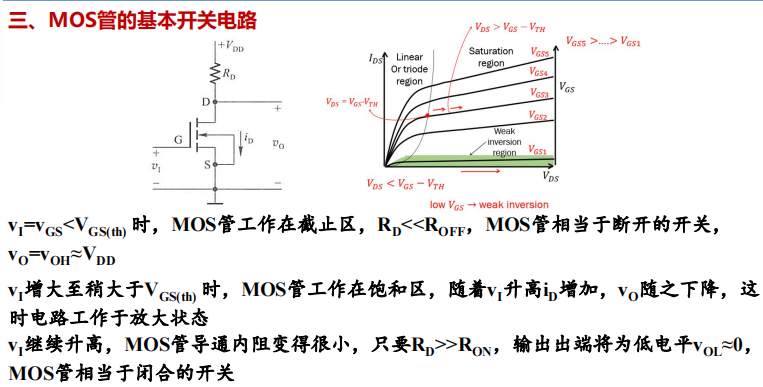
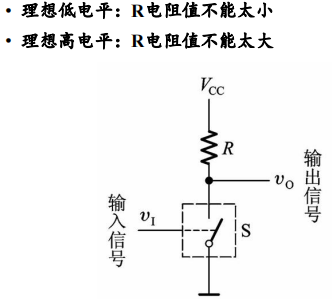
2.3 Basic switch circuit
3. Gate Circuits of CMOS
3.1 CMOS Inverter
- CMO 反相器(非门)工作原理
为了杜绝以上这种电阻大小的矛盾问题,我们构造如下CMO互补电路:
注意从上到下的CMO分别为PMOS、NMOS,不能颠倒!
如果要正常工作,高电平一点要高于$V_{IH}$,低电平一定要低于$V_{IL}$。
而在这两者之间,两个CMOS均导通,该区域具有非常高的增益(输入电压$V_{IN}$的微小变化会引起输出电压$V_{OUT}$的较大变化),且电压传输特性曲线(VTC)几乎是一个阶跃函数。
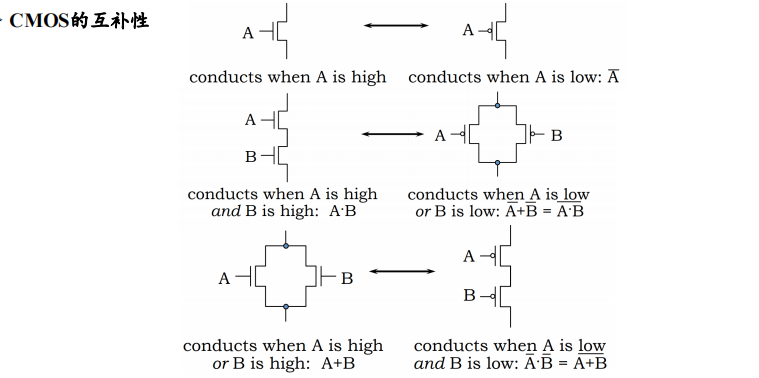
The Complementary of CMOS
Tricks:
- $P\leftrightarrow N $
- 串联 $\leftrightarrow$ 并联
3.2 The Other Kinds of CMOS Gate Circuit
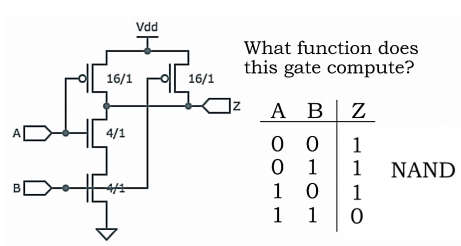
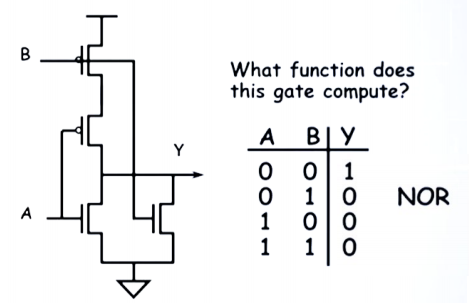
1. Logic Gate
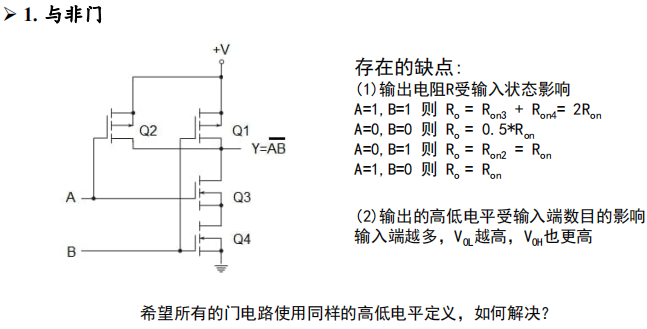
- CMOS门电路天然是反相的,所以你不可能使用一个CMOS门电路构建正逻辑,例如与门。
- 其实这很好理解,比如只看下面接地的部分,一但满足导通条件(1)势必会带来输出结果为0,反相就是这么来的。
- 注意,不能将PMOS与NMOS颠倒,那样只会使得两者在输入为高低电平时都导通
,没有意义。
缺点与改进
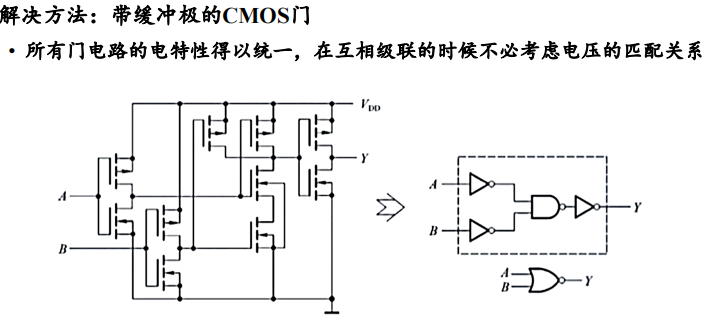
其实就是对每一个输入、输出进行标准化操作,我们在在电路的每一个输入端、输出端各增设一级反相器(这些具有标准参数的反相器被称为缓冲器)
但值得注意的是,在添加缓冲器之后,电路的逻辑功能也会发生相应的变化
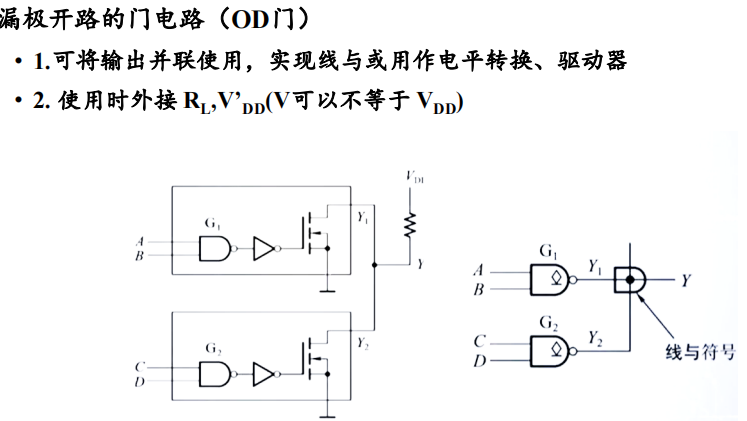
2. OD Gate (Open-Drain Output Gate)
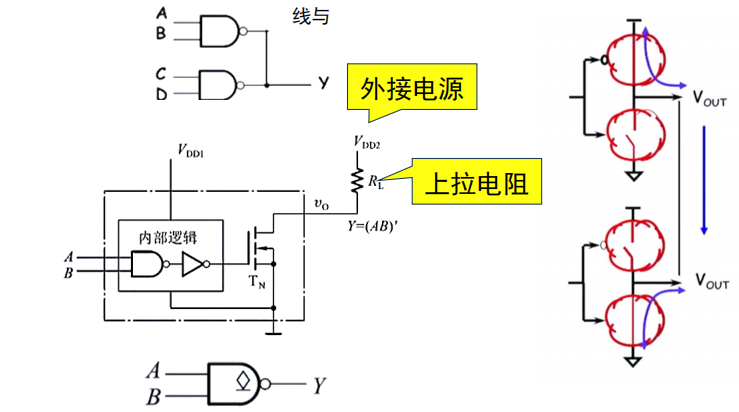
在CMOS电路中,为了满足输出电平变换、吸收大负载电流以及实现线与连接等需要,将输出级电路结构改成一个漏极开路输出的MOS管,构成OD门。
当我们要实现线与操作时,如果还是使用上面的电路,直接连接到一起会出现短路(当上下均输出为高电平的时候)的现象,而在这里,我们将输出级改为漏极开路输出,这样即使均为高电平输出,也会有保护电阻$R_L$存在,不会出现问题。
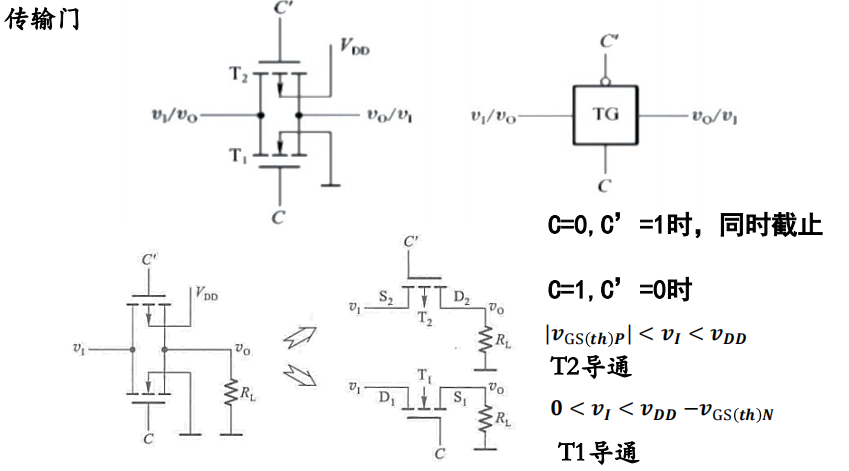
3. CMOS TG (Transmission Gates)
CMOS传输门其实就相当于一个开关,如下就是保证只有当$C=1$时才能导通输入的信号。
注意:由于$T_1,T_2$管的结构形式是对称的,漏极源极也没有什么本质之分,因此CMOS传输门属于是双向组件,输入端输出端可以交换使用。
4. Output Buffer
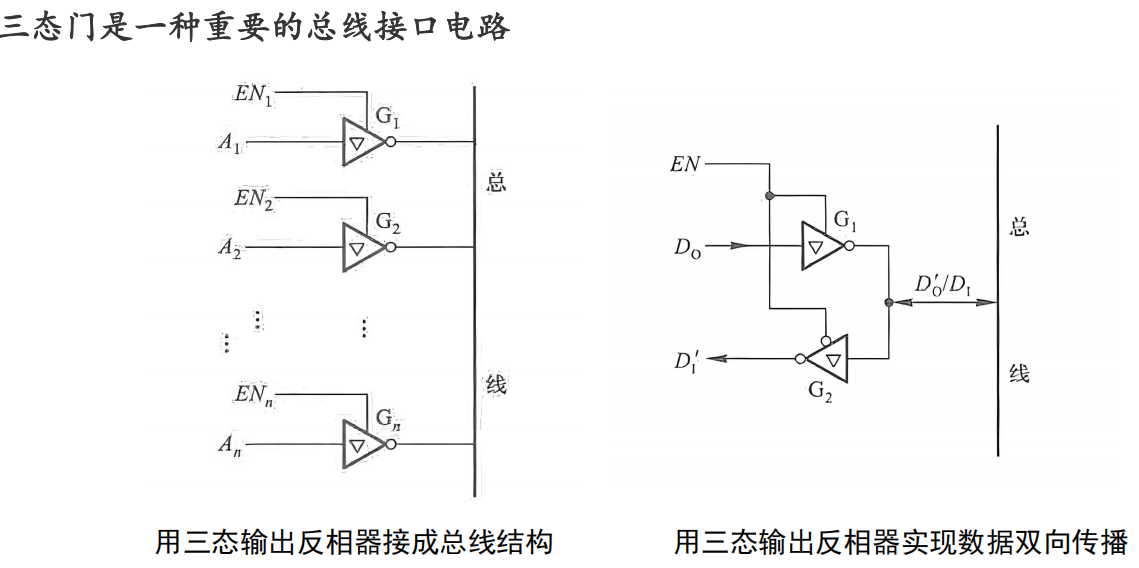
三态输出的CMOS门电路的三个状态:高电平、低电平、高阻态。
因为这种电路结构总是连接在集成电路的输出端,所有又称输出缓冲器(Output Buffer)。
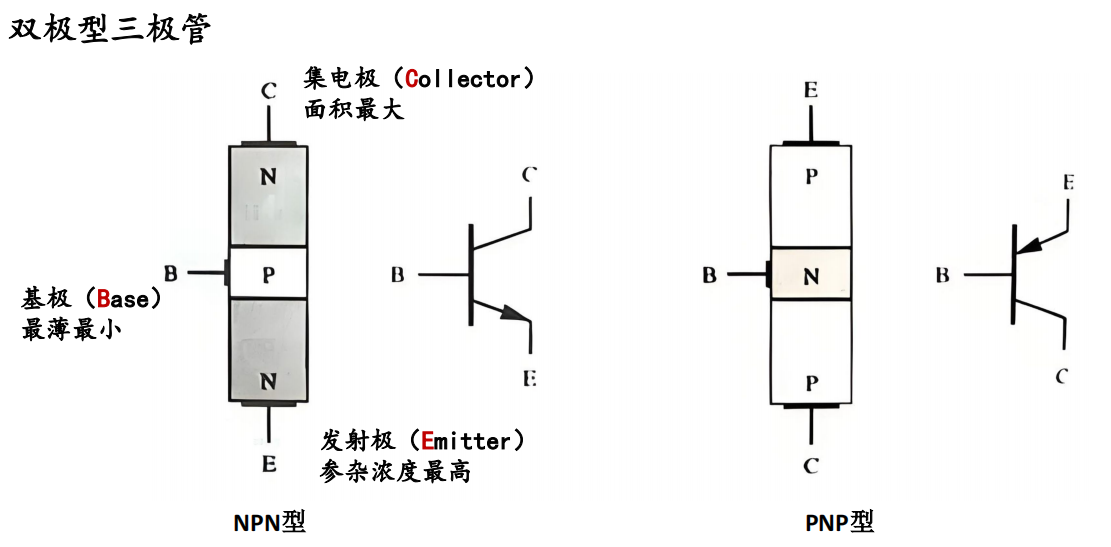
4. TTL
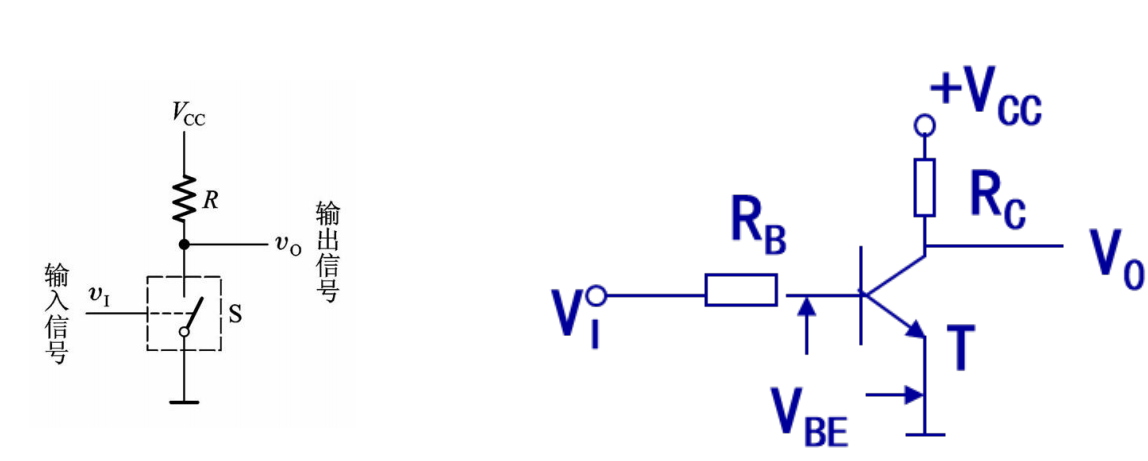
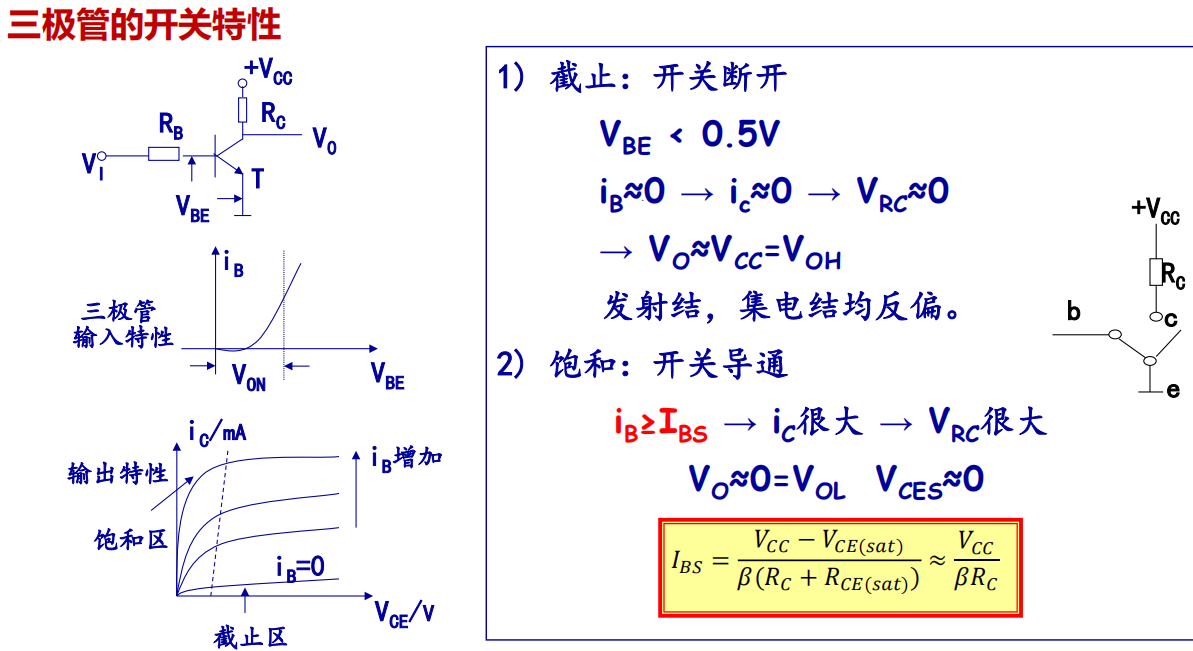
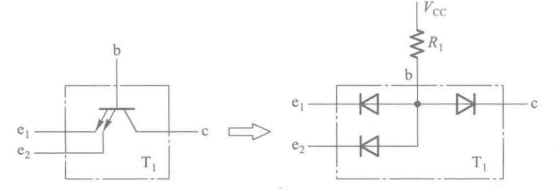
4.1 Triode
4.2 TTL NOT Gate
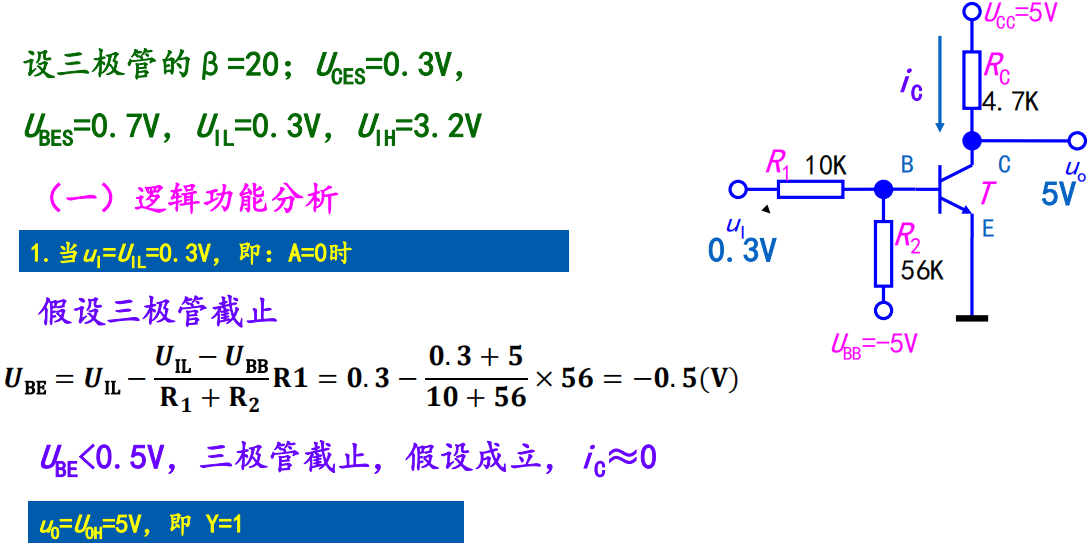
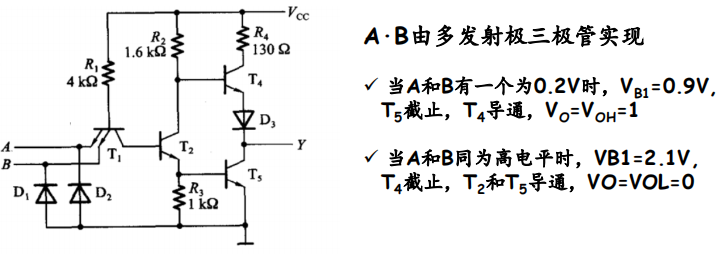
1. Circuit structure and working principle
输出为高电平
- 首先$T_1$一定是饱和导通的$\Rightarrow V_{B1}=0.9V$
- 在$T_1$的集电极回路中,无论$T_2$导通与否,$I_C$都极小(未导通时由于电阻为$R_2$与$T_2$的$BC$反向电阻之和,电阻极大,故电流$I_C$极小),判定为深度饱和,由图像可知$V_{CE}\rightarrow 0$,故$T_2$的发射极不可能导通。
- 因此$V_{E2}\rightarrow 0$,而$V_{C2}$为高电平,故$T_5$截止,$T_4$导通,输出为高电平。
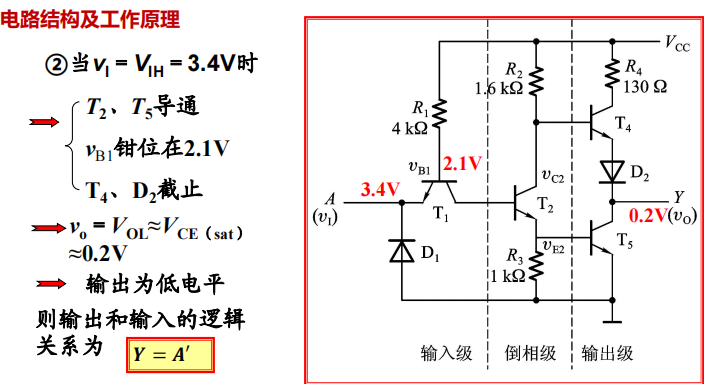
输出为低电平
- 首先假设$T_1$导通,则此时$V_{B1}=3.4V+0.7V=4.1V$,而此时又$T_2,T_5$又一定导通,如此判定$V_{B1}=0.7V+0.7V+0.7V=2.1V$。矛盾,则假设不成立,$T_1$截止!
- 所以此时$T_2,T_5$导通,而此时$V_{C2}$降低,$V_{E2}$增加,$T_4,D_2$截止。故输出为低电平。
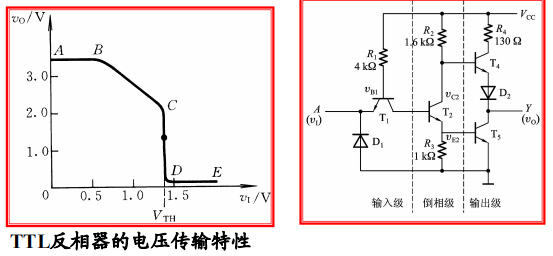
2. Voltage transmission characteristics
$AB$ :截止区
$BC$:
分析为什么是线性:
\[V_{E2}=V_{I}-0.7\] \[由于在放大区\Rightarrow I_{C2}\propto I_{E2}=\frac{V_{I}-0.7}{R_2}\] \[V_O=V_{CC}-I_{C2}R_2-1.4\]显然是$V_O$是关于$V_I$的线性减函数。
$CD$:
$DE$:
3. Input Noise Tolerance
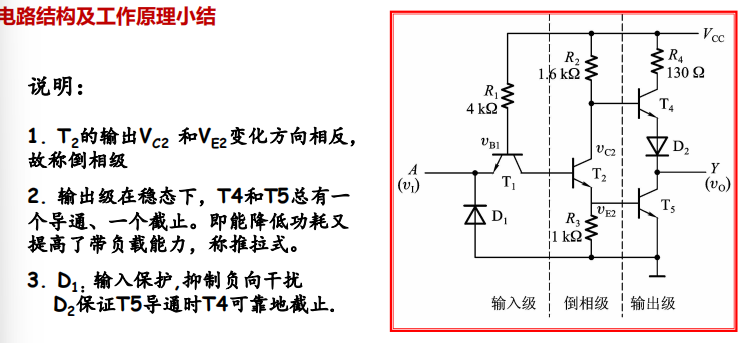
4. Conclusion of the Structure & Principle
$T_2$的倒相级:
- 当$T_2$截止时,$V_{E2}\rightarrow0$,$V_{C2}\rightarrow V_{CC}$
- 当$T_2$导通时,可通过上下的分压分析,电流越来越大,两者越来越解决,一减一增
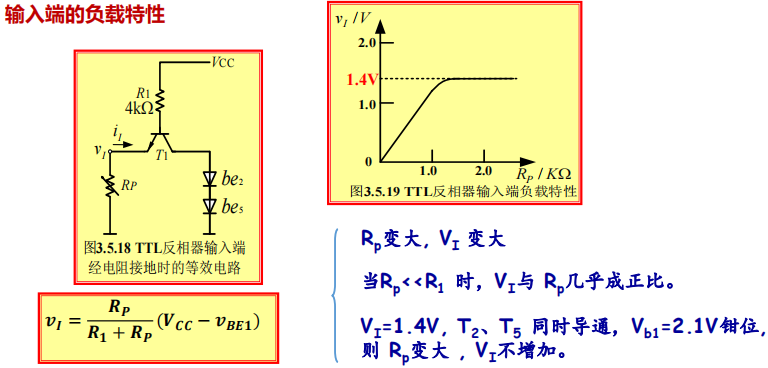
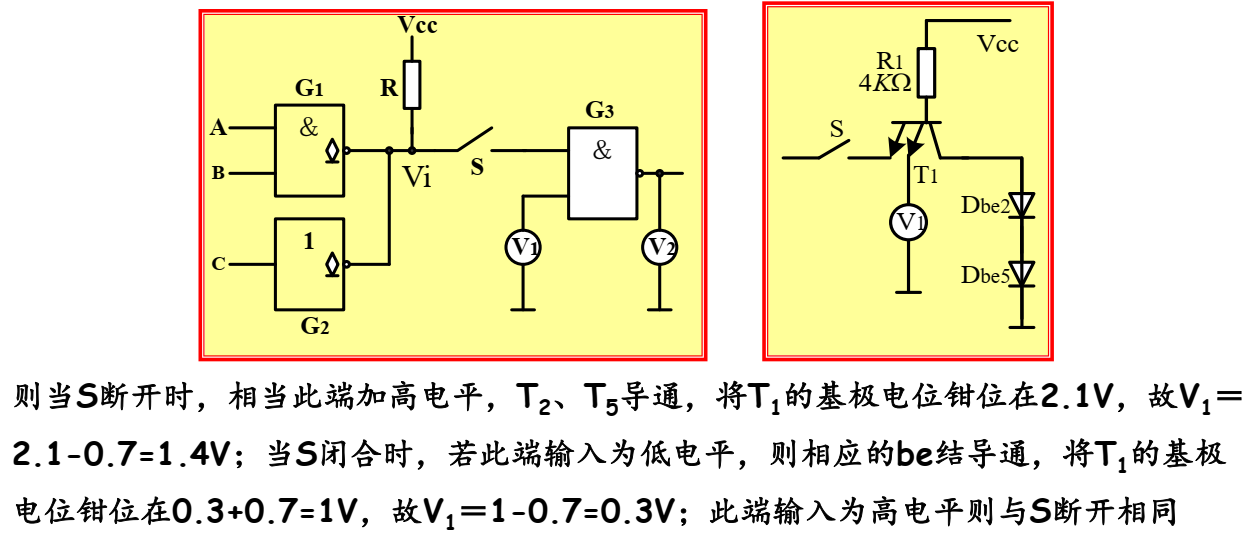
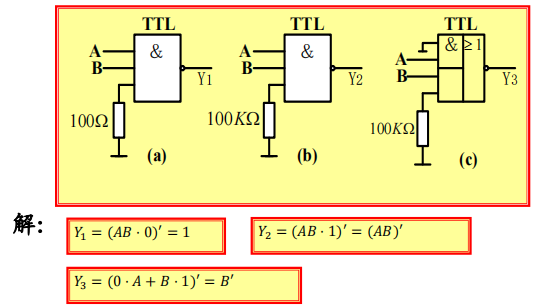
5. Input Load Characteristics
注意这里有一个特例,就是当为与门时,只要有一个输入端是低电平,就会将电压钳制,另外的端口即使接的是大电阻也不能等效为高电平
4.3 The Other Gates of TTL
与非
- 只要$A$或者$B$有一个为低电平,就能将$T_1$“钳住”——从而使得$T_2,T_5$截止,$T_4$导通输出高电平。
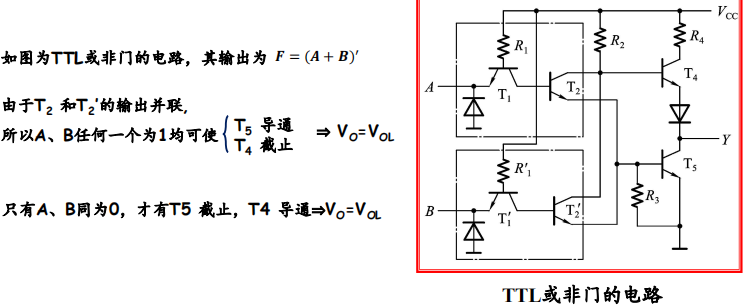
或非
- 相当于接了两个输入级和倒相级,任何一个为高电平都能使得最终输出低电平。
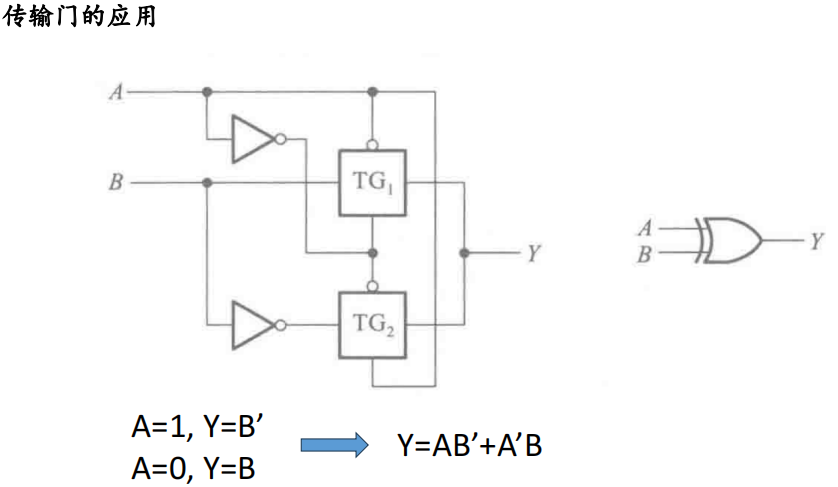
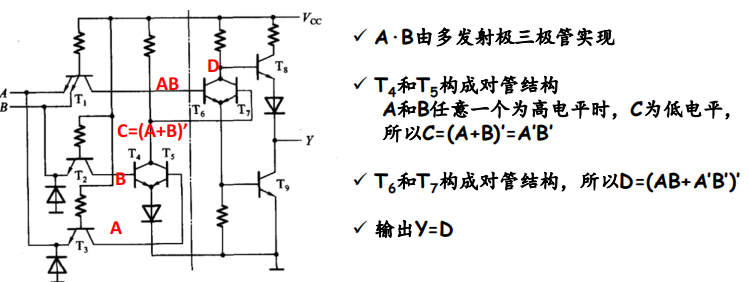
异或
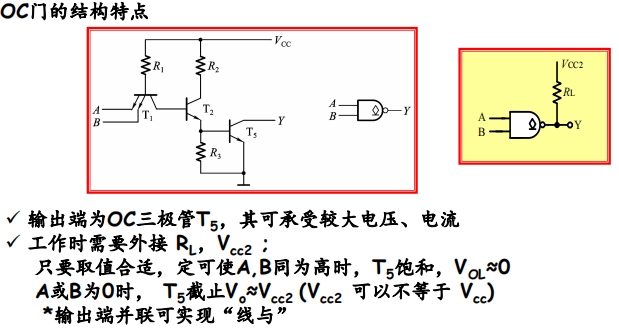
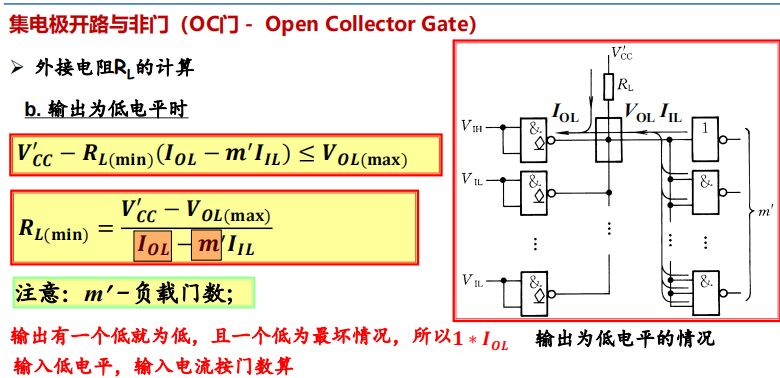
4.4 OC Gate (Open Collector Gate)
原本推拉式输出电路结构的局限性:
- 不能线与
- 不能满足大电流与高电压负载要求
- 输出的高电平的值是固定的
(其实与上面普通CMOS电路的缺点一致,这也是为什么后来有了OD门)
OC门结构
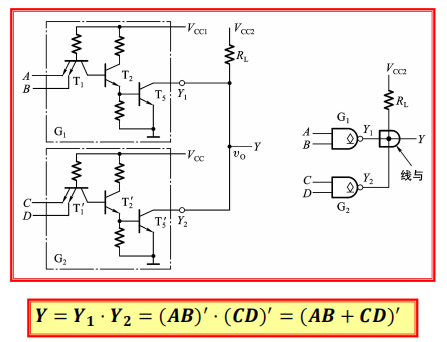
线与的实现
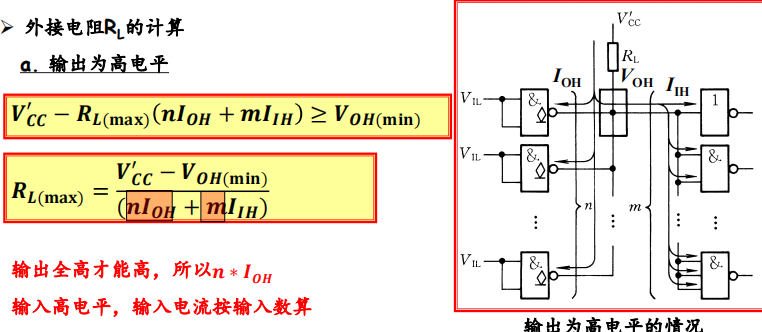
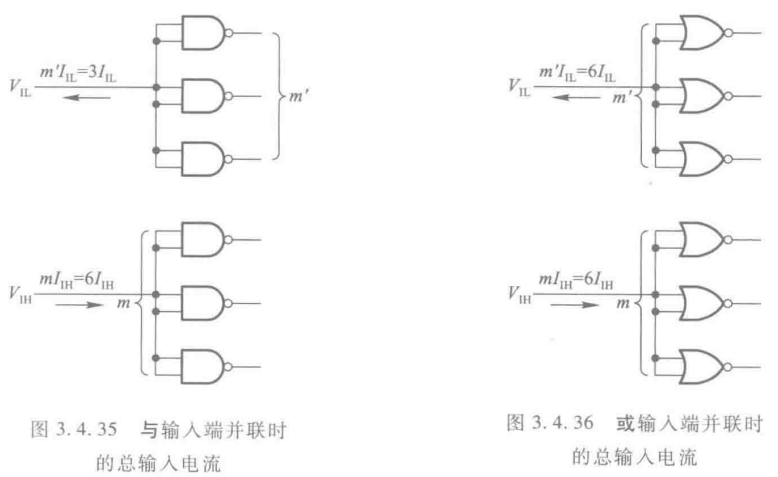
外接电阻$R_L$的计算
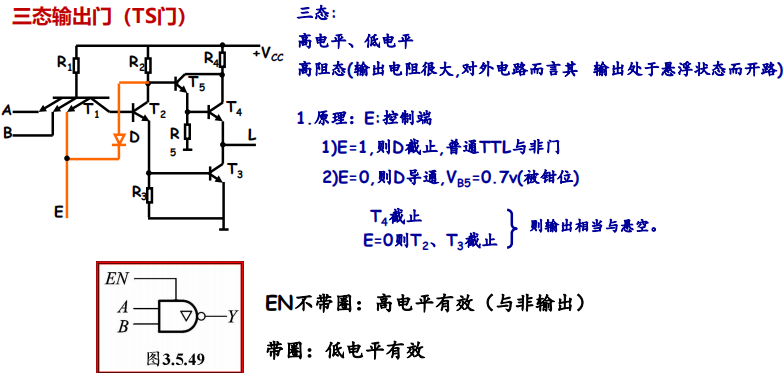
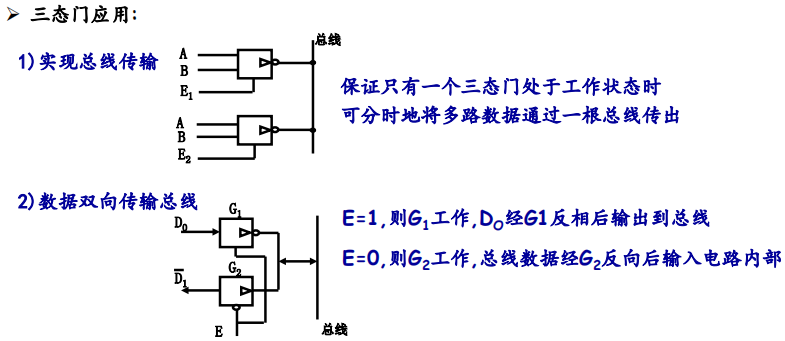
4.5 TS Gate
TTL中的三态门,和3.2.4中的CMOS的三态输出门一致。
还是相当于有一个使能端$EN$,当图标不带圈时,说明高电平对应正常的与非输出!!!
原理很简单,相当于$E$极再并联一个二极管$EN$,由$EN$的导通与否来钳制电压。