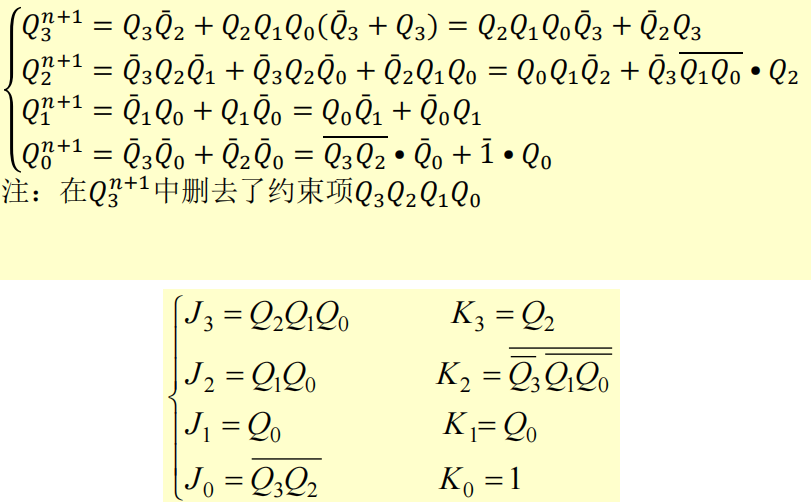Post

Sequential Logic Circuits

Posted Updated
By Young Friday
11 min read
Sequential Logic Circuits

6a13123e348f81830d2e53cd636e9c5

时序逻辑电路

1. 时序逻辑电路的基本概念

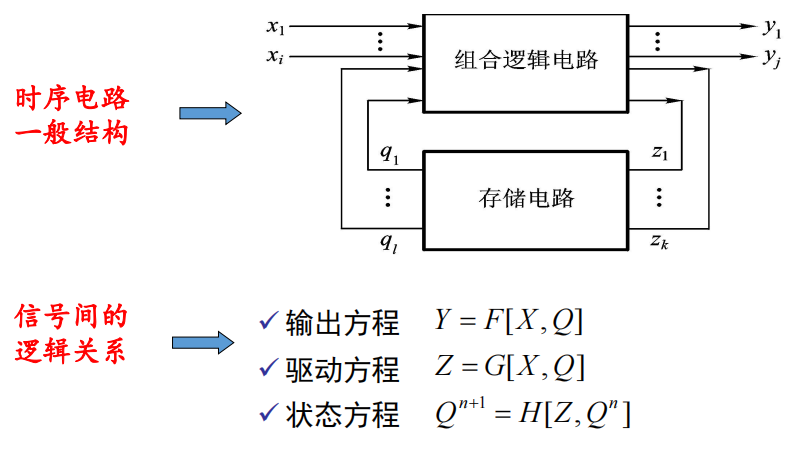
1.1 结构与特点

image-20241106225518922

  • 功能上：不仅与该时刻输入有关，还与电路原状态有关
  • 结构上：由组合电路和存储电路组成；存储电路的输出反馈到输入端。

1.2 分类

  1. 按动作特点：
    • 同步 有统一时钟，状态变化与时钟同步
    • 异步 无统一时钟，状态变化不同步
  2. 按输出信号：分为米里型与莫尔型
  3. 按通用性：分为通用时序电路与一般时序电路

2. 时序逻辑电路的分析方法

2.1 分析步骤

  1. 根据给定时序电路图写出各逻辑方程式
    1. 写驱动方程 – 就是各个触发器的输入
    2. 推导状态方程 – 驱动方程代入触发器特征方程
    3. 写输出方程
  2. 列出状态表，画状态转移图或者时序图
  3. 说明电路的逻辑功能

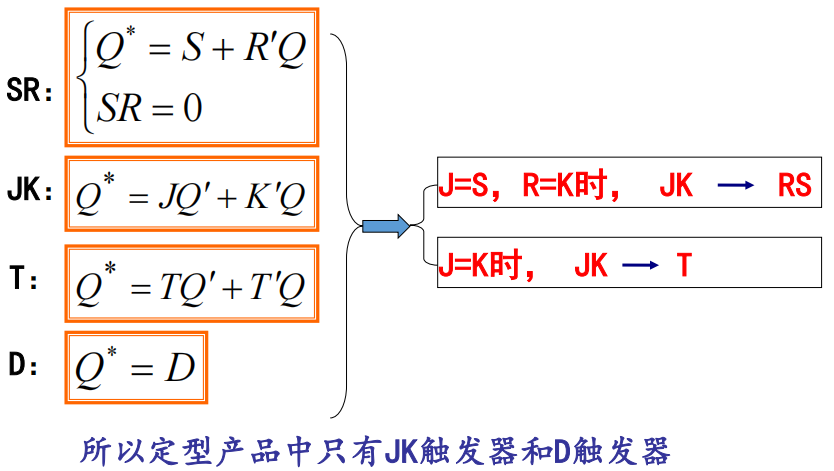
2.2 一些触发器的回顾

image-20241106230603916

其实SR就相当于JK再加一个条件–JK=0

3. 常用时序逻辑电路

寄存器

  • 功能：可寄存一组二进制数值或者代码的电路
  • 结构：
    1. 具有置0或者置1功能的触发器
    2. 1个触发器存1位二进制代码，存n位就需要n个触发器
  • 分类：
    1. 按功能：数码寄存器、移位寄存器
    2. 按数码存取方式：串行寄存器、并行寄存器

数码寄存器

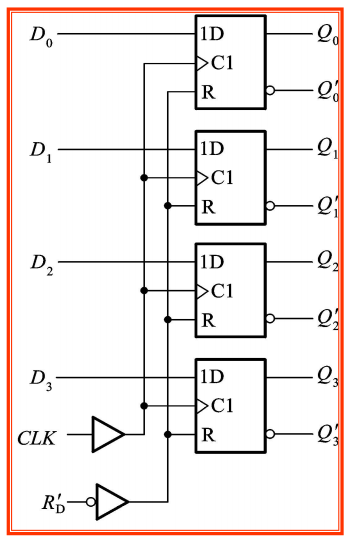
74HC175

image-20241111202222721

  • 边沿D触发器构成
  • 在时钟上升沿，Q随D改变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

module hc175(
	input wire clk;   	  
    input wire reset,	  //异步复位信号
    input wire [3:0] d,   //数据输入
    output reg [3:0] q,   //数据输出
    output reg [3:0] nq   //返向输出
);
    
    //在时钟的上升沿触发
    always@(posedge clk or posedge reset) begin
        if (reset) begin
            q<=4'b0000;
            nq<=4'b11111;
        end else begin
            q<=d;
            nq<=~d;
        end
    end
endmodule

移位寄存器

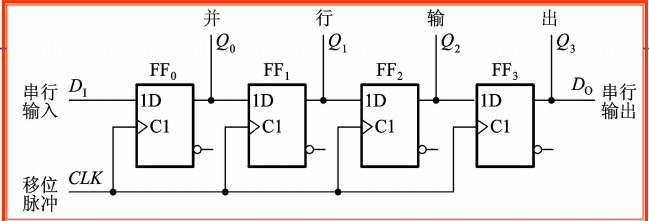
  1. 单向移位寄存器

    image-20241111202456585

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

    module serial_left_shift_register(
    input wire clk,
    input wire reset,
    input wire serial_in,
    out reg [3:0] q  //输出的4位数据
);
    //异步复位和左移
    always @(posedge clk or posedge reset) begin
        if(reset)begin
            q<=4'b0000;
        end else begin
            q<={q[2:0],serial_in} //左移，最低位输入serial_in
        end
    end
endmodule

  2. 双向移位寄存器

    1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

    module bidirectional_shift_register(
    input wire clk,
    input wire reset,
    input wire left_in,  //左移输入数据
    input wire right_in, //右移输入数据
    input wire direction, //方向选择
    output reg [3:0] q
);
    //异步逻辑和移位逻辑
    always @(posedge clk or posedge reset) begin
        if(reset)begin
            q<=4'b0000;
        end else begin
            if(direction)begin
                //右移
                q<={right_in,q[3:1]}
            end else begin
                //左移
                q<={q[2:0],left_in}
            end
        end
    end
endmodule

计数器

  • 功能：用以统计输入脉冲CP个数的电路
  • 分类：
    1. CP引入方式：
      • 同步
      • 异步
    2. 计数功能
      • 加计数
      • 减计数
      • 可逆计数
    3. 计数体制
      • 二进制
      • 非二进制
    4. 构成方式
      • JK
      • D
      • RS
  • 应用：计数；分频；定时；序列信号发生器……

同步计数器

同步二进制计数器-加法
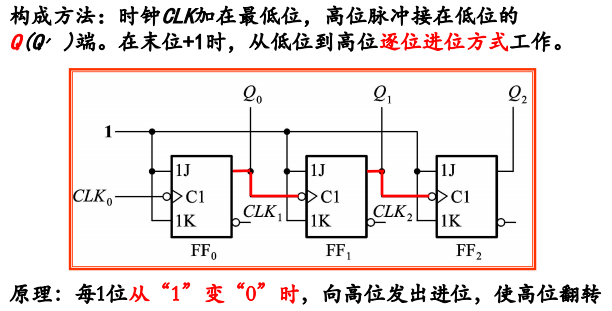
  • 多位二进制数的末位加1就翻转
  • 第i位以下皆为1时，第i位翻转

可以采用T触发器构成多位二进制加法器

  • T触发器，T=0时保持，T=1时翻转
  • $Q^*=TQ^{\prime}+T^{\prime}Q$

  1. 驱动方程

    \[T_i=Q_{i-1}Q_{i-2}...Q_{0}\\ T_0\equiv1\]

  2. 状态方程

    \[Q^*=TQ^{\prime}+T^{\prime}Q\]

  3. 状态方程代入即可。

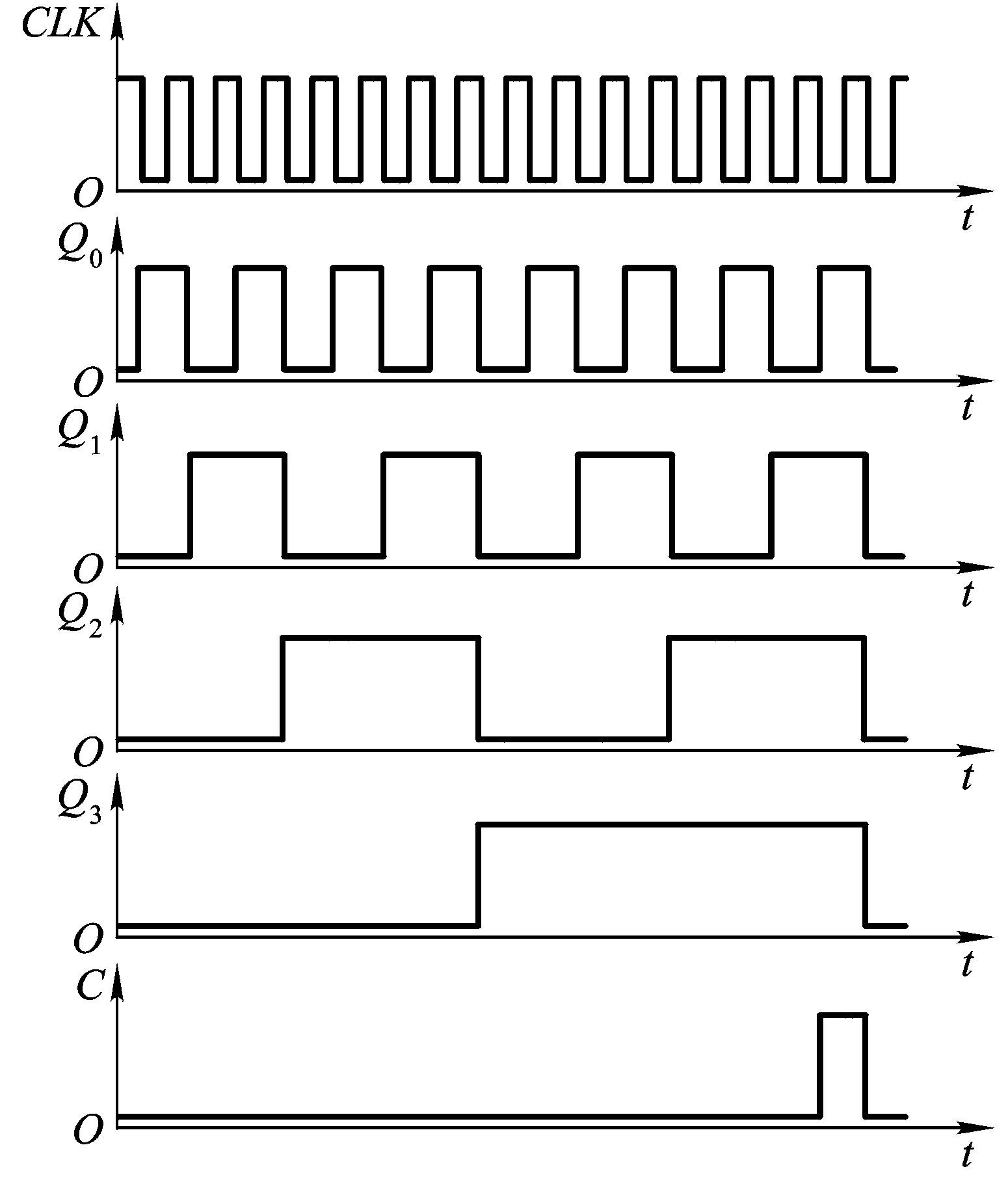
一个4位同步二进制加法计数器其实能实现两个功能

  1. 16进制计数器（我们将计数器中能计到最大的数称为计数器的容量）
  2. 分频功能（见下图）

image-20241114000937005

同步二进制计数器-减法
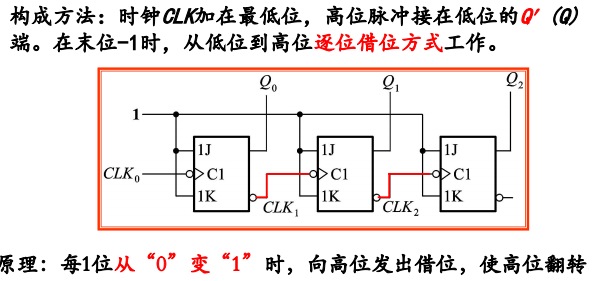
  • 末位减1就翻转
  • 如果第i位以下皆为0，第i位翻转
同步二进制计数器-可逆计数器

增加了一个输入端口用来控制是加法计数还是减法计数

同步十进制计数器-加法

原理很简单，在四位二进制计数器基础上修改，当计到1001时，则下一个CLK电路状态回到0000即可。

image-20241120223454943

同步十进制计数器-减法

原理：对二进制减法计数器进行修改，在0000之后跳变为1001

image-20241120224707741

异步计数器

异步二进制计数器

image-20241120231759218

image-20241120231808677

异步十进制计数器

image-20241120233032339

$ 1110\rightarrow 0001 \rightarrow 1001 \rightarrow 0000 $

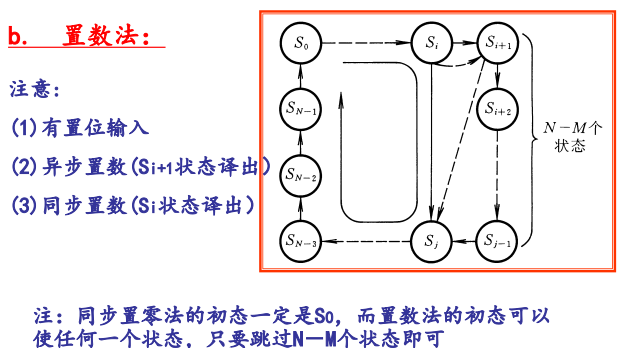
任意进制计数器的构成方法

从$N\rightarrow M$ 进制转换

  1. $M<N$

    N进制计数器，跳过 (N-M)个状态，变成M进制计数器

    • 置零法

      1. 异步置零（$S_M$ 状态译出）

        有一个暂态，容易出现还没置零完毕置零信号消失，所以有以下改进方式——给置零信号增加SR锁存器，如此一来，在下一个时钟信号来临之前， $R_D^{\prime}=0 $ 恒成立

        image-20241121000851784

      2. 同步置零 （$S_{M-1}$状态译出）

    • 置数法

      image-20241121001717229

  2. $M>N$

    采用多片级联组合的方法实现任意进制计数。

    • $M=N_1N_2$ 可采用串行进位方式/并行进位方法
      1. 串行进位方法：以低位片的进位输出信号作为高位片的始终输入信号。
      2. 并行CP方法：以低位片的进位输出信号作为高位片的控制信号（使能），两片的CP同时接计数输入。
    • 当$N_1$，$N_2$ 不等于 $N$ 时，可先将 $N$ 进制计数器分别接成 $N_1$ ,$N_2$ 再按照串行或平行方式连接。
    • 当$N$为素数时，不能分解为$N_1$ 和$N_2$ ，采用整体清零or整体置数的方式
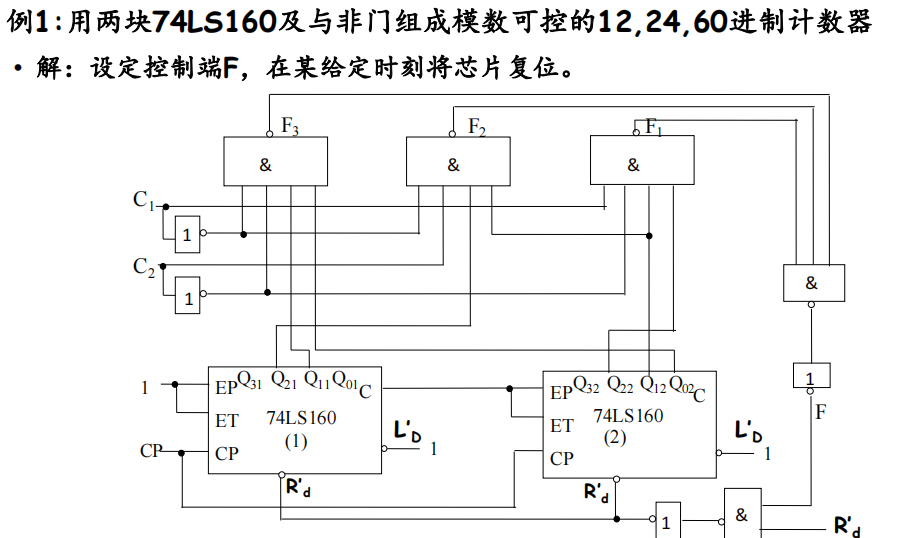
      1. 整体清0：将2片计数器连接成大于$M$的计数器，在计到$M(M-1)$时（同步）译出清0信号 $C_r^{\prime}=0$，将两个计数器同时清零。
      2. 整体置数：将2片计数器接成大于$M$的计数器，然后选定某一状态译出置数信号$LD’=0$ ，将两个计数器同时置入适当状态，跳过多余状态。

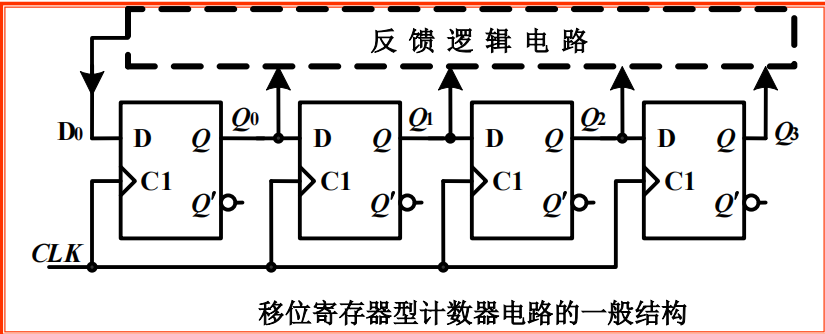
移位寄存器型计数器

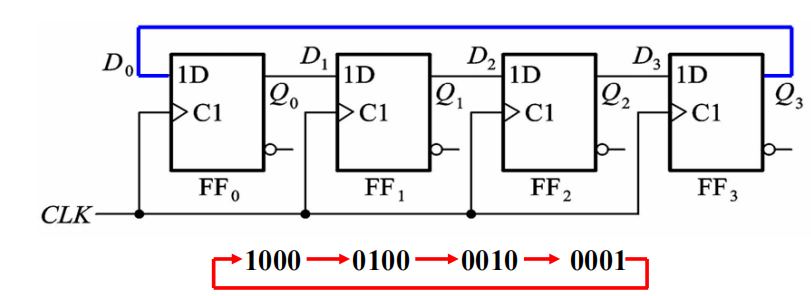
  1. 环形计数器

    image-20241129221320606

    • 优点：电路结构简单，有效状态只含有一个1（或0），不需要另加译码电路
    • 缺点：状态利用率低，$2^4=16$ 个状态中只用了4个状态（2^n-n个没用）

  2. 扭环形计数器

    • 先看一种简单的——直接在最后取一个反：

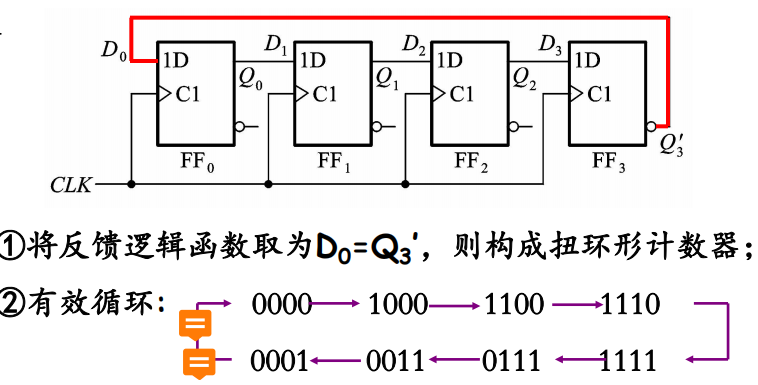
      image-20241129221724221

      • 优点：状态利用率提高一倍，每次状态更新只有一个触发器改变状态，因此译码时不会产生竞争冒险
      • 缺点：状态利用率低。16个只用了8个。

    • 再看一种稍微复杂一点的，其实也可以参考卫星导航中的移位寄存器伪随机码

      image-20241129225457272

      根据状态要求修改反馈逻辑，实现能自启动的环形计数器和扭环形计数器

4.时序逻辑电路的设计方法

4.1 由触发器和门电路设计同步时序电路

image-20241119193251177

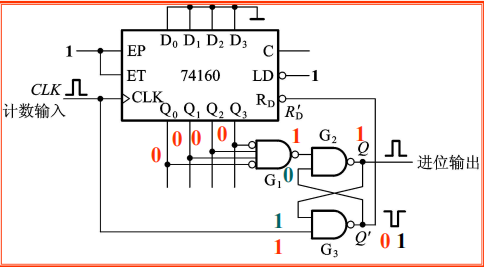
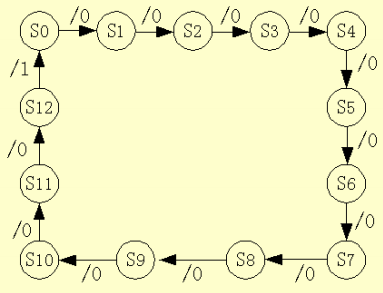
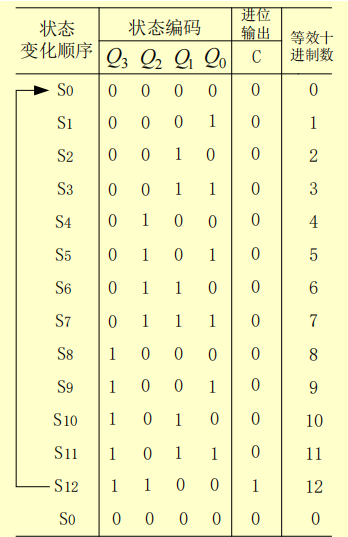
e.g.1 设计一个带有进位输出端的十三进制计数器

  1. 设定状态，导出对应状态图或者状态表

    选择$M=13$

    image-20241204231606155

  2. 状态化简：不能简化

  3. 状态分配：取$n=4$，取其中的$13$个状态，按十进制数取$0000\sim 1100$十三个状态

    image-20241204232324977

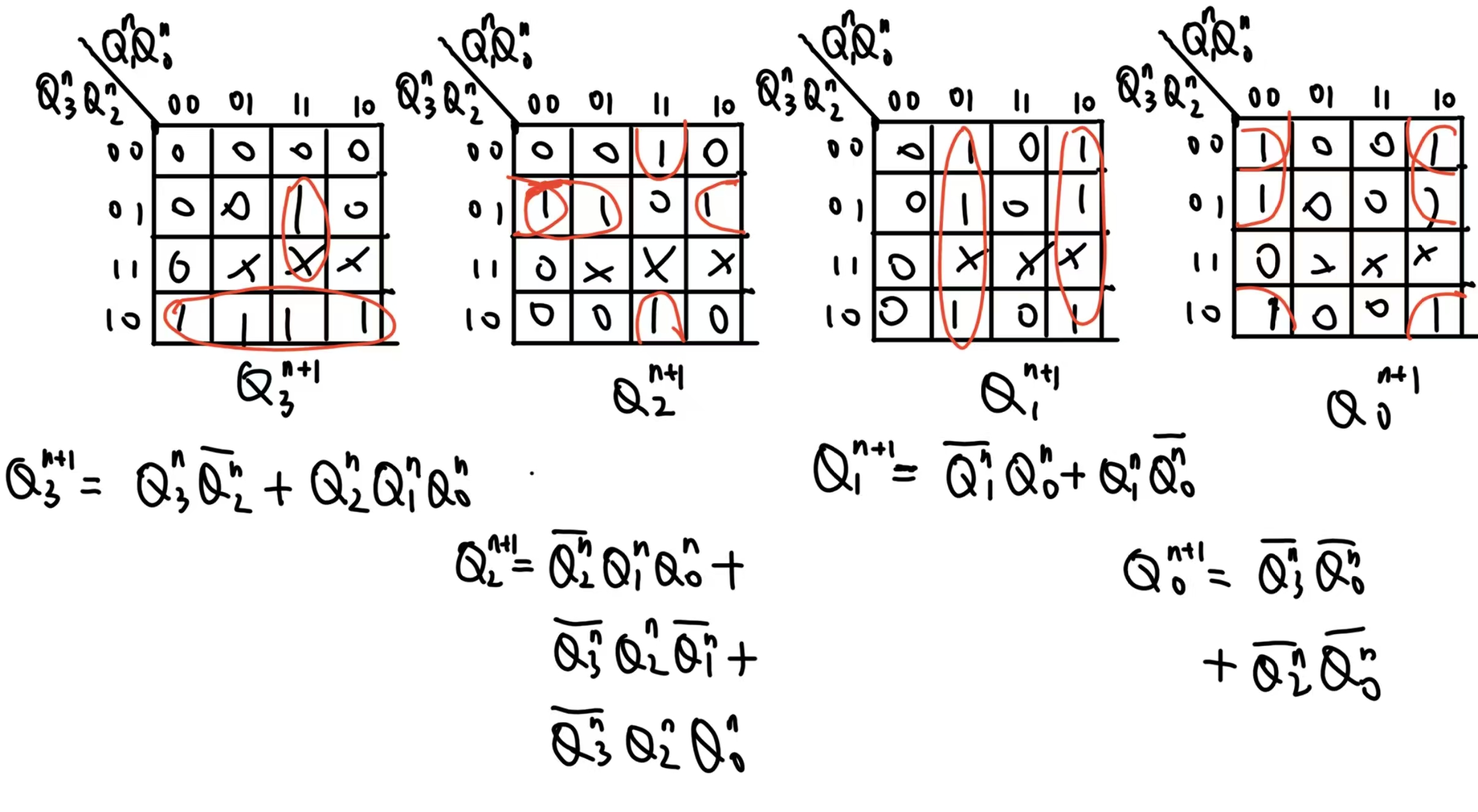
    各个输出段绘制卡诺图

    a9e2d4f455d5ac10493c092a21ce81e

    \[C=Q_3Q_2\]

  4. 选触发器：选用JK触发器

  5. 推导出相应触发器状态、驱动、输出方程：

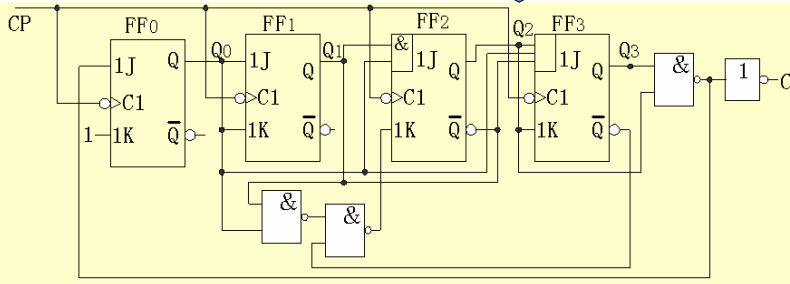
    \[Q^{n+1}=J\overline{Q^n}+\overline{K}Q^n\]

    image-20241205001026447

  6. 画逻辑图

    image-20241205001055016

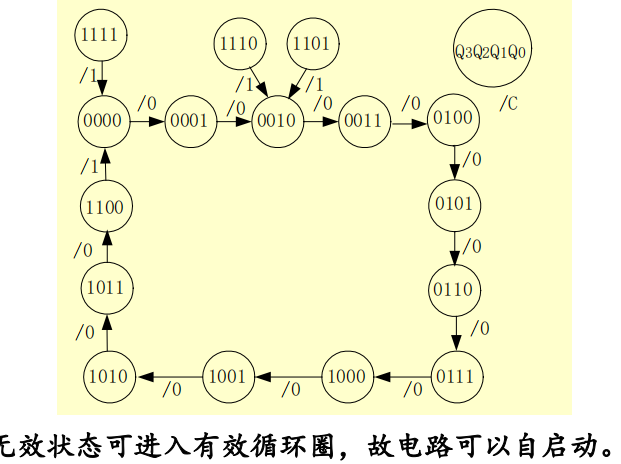
  7. 检查自启动：将无效状态代入状态方程，推导能否进入有效圈

    image-20241205001346416

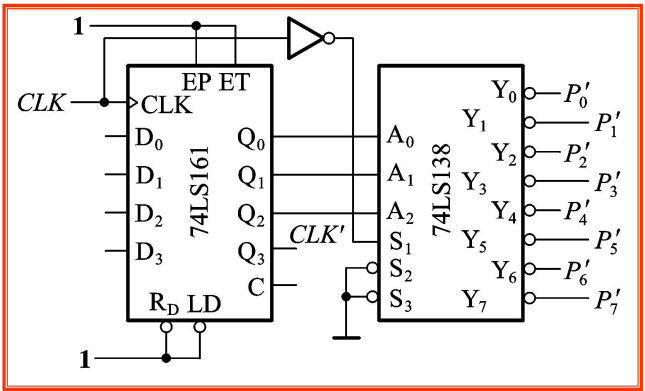
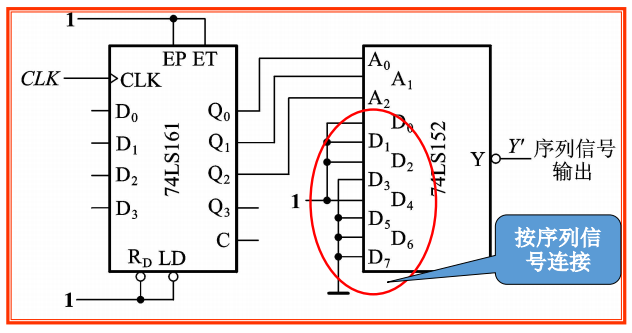
4.2 由中规模集成电路分析设计时序电路

  1. 可变进制计数器

    image-20241219234030215

    image-20241219234044514

  2. 顺序脉冲发生器

    • 计数器+译码器

    image-20241219234130733

    • 环形移位寄存器

    image-20241219234221127

  3. 序列信号发生器

    • 计数器+数据选择器

      image-20241219234525242

    • 带反馈的移位寄存器 (只能在没有重叠的时候用)

      image-20241220001812798

      image-20241220002034534

      • 中间均用D触发器相连，需要考虑的就是反馈输出到$Q_0$的D触发器表达式怎么写，以使得下个时钟沿输入正确的序列

    • 由触发器构成（重叠的时候可以使用）

      image-20241220003449777

      这里三个串联触发器的作用实际上就是三位二进制计数器

NOTES, VLSI
Logic Circuits
This post is licensed under CC BY 4.0 by the author.