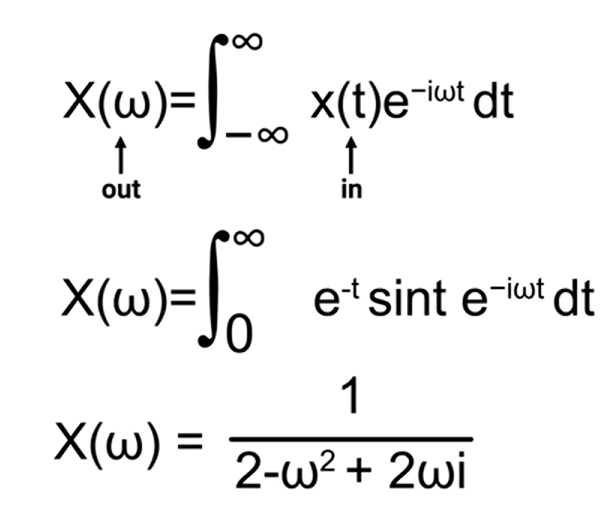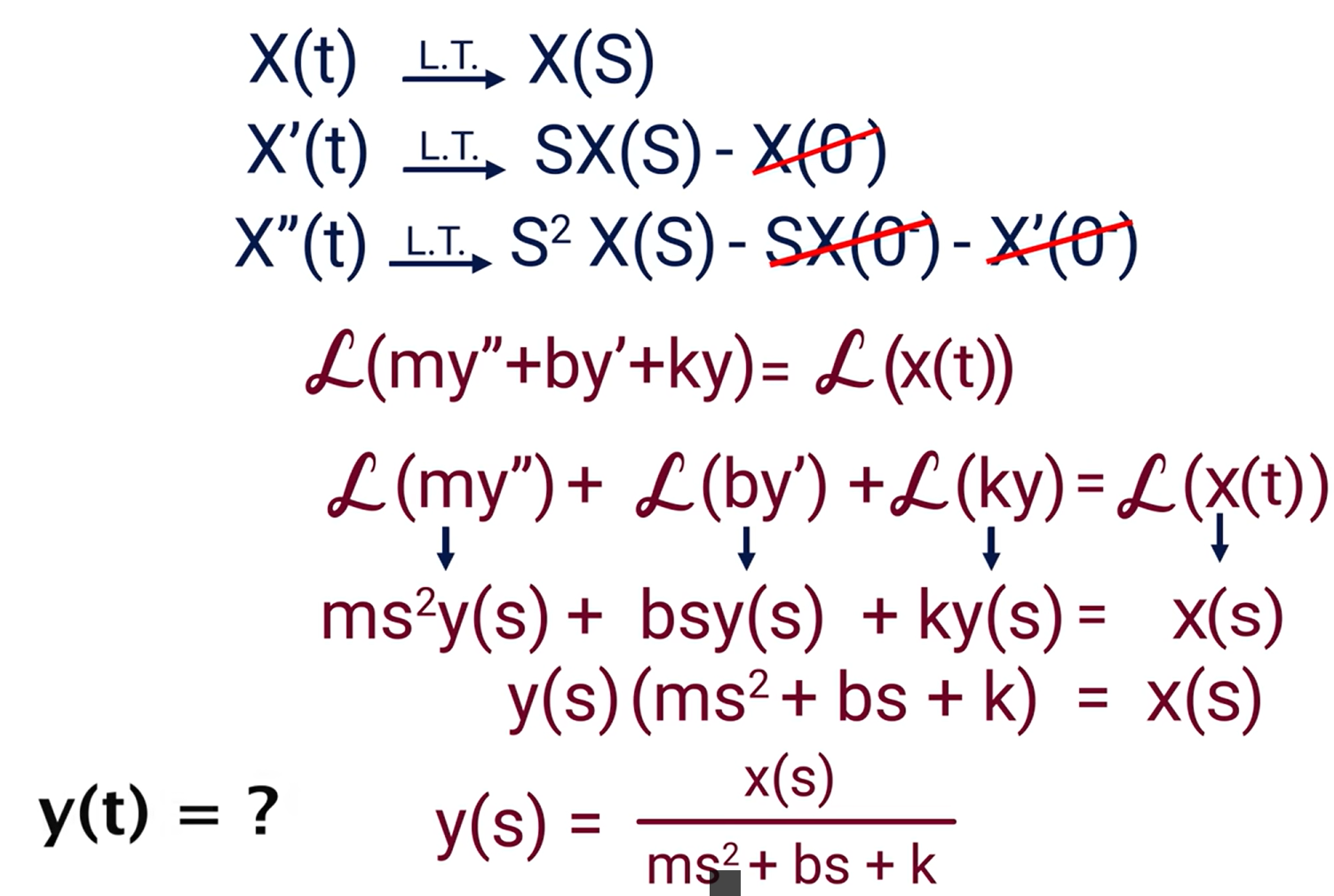The Mystery of the Fourier and Laplace Transforms
The Mystery of the Fourier and Laplace Transforms
本文将揭晓傅里叶变换与拉普拉斯变换的奥秘，以及为何拉普拉斯变换在经典控制理论中能大显神通？且听我慢慢道来……
- 傅里叶变换与拉普拉斯变换究竟在折腾啥？咱们何苦呢？
- 为什么我们在经典控制理论中会选中拉普拉斯变换？
- 为啥我们就一直关注闭环特征方程的零点就完事了？
Context
复变函数与积分变换是大二上学期的课程，恰逢周三晚上，常觉困意袭人，无聊至极，索性翘课抄作业上传云盘，屡试不爽。考前突击2天，自以为已经通晓其奥义，早早做完卷子，怡然自得。殊不知期末成绩赫然87。本以为被复变支配的时光到此为止，此后你我二人井水不犯河水，自此分道扬镳。
然而，缘分未尽，大二下学期迎来自动控制原理，经典控制理论又是拉普拉斯变换的realm……但好像感觉不理解为啥变换也照样能做题，吸取教训，没有翘课，平日认真作业复习教案，最终又是欣然就义——您猜怎么着？喜提85！
本学期升至大三，短暂脱离复变函数与积分变换的羁绊（应该说本学期是线性代数的realm，乐，又是一短板）。但想着下学期还有究极破防好课——数字信号处理，所谓傅里叶变换的realm。为了防止重蹈覆辙，借着现代控制理论老师布置的总结经典控制理论的作业，我还是提前找回这羁绊，以叙旧情，斗胆提笔研究一下一直蒙在鼓里的Fourier与Laplace两位前朝元老。
Fourier Transform
Interesting History
要想搞清楚拉普拉斯变换，就得先搞清楚傅里叶变换是个什么事情，但关于这两者的提出时间的先后还具有争议。这两位老哥都是法国人，傅里叶是在研究热力学问题时引入傅里叶变换，而拉普拉斯是在研究概率论时正式引入拉普拉斯变换。好巧不巧，傅里叶那篇论文的评委中就有拉普拉斯。拉普拉斯和蒙日两位大佬对这位年轻人赞赏有加，而另一位巨擘——拉格朗日却极力反对这种方法，这也最终导致这篇论文没有成功发表。
Definition
\[F\left( \omega \right) =\mathscr{F} \left[ f\left( t \right) \right] =\int_{-\infty}^{+\infty}{f\left( t \right) e^{-i\omega t}dt}\]工程上一般用的都是广义傅里叶变换，所以我这里就直接从广义变换开始（其实是数学不好）。
What’s Fourier Transform doing?
参见上面的式子，我虽然没去过几节复变课，但还是依稀记得老师说啊，傅里叶变换好啊，好就好在它把“时域（$t$）”转换到“频域（$\omega$）”上来啦——我估计大家也没少听这句话，书上也是几乎啥也没讲，上来直接展示定义，开始积分变换！以至于最后很多学生积分变换算的一个比一个6，但是不知道为了啥（但遗憾的是，我不仅不懂，算的也差）。反正学完了，我脑子里唯一的概念就是——从一个$f(t)$变成了$F(\omega)$，至于能干啥？为啥？别问，问就是不知道，读书人的事少打听，帅就完事了。
我们实际一点，别想搞数学那帮巨擘那样虚无缥缈，其实从工程上来说，比如我接受到一连串复杂正余弦信号混合的电信号$f(t)$，但其实我关心很大程度上不是$f(t)$本身随时间变化的波形，我关心的其实是其中承载了多少不同$\omega$的信号，它们具体有多少呢，因为信息基本都承载在$\omega$中。那有啥办法能把每个$\omega$从一堆混乱的信号中分辨出来其有多少呢？我们从另一个人尽皆知的例子谈起——
Orthographic Projection
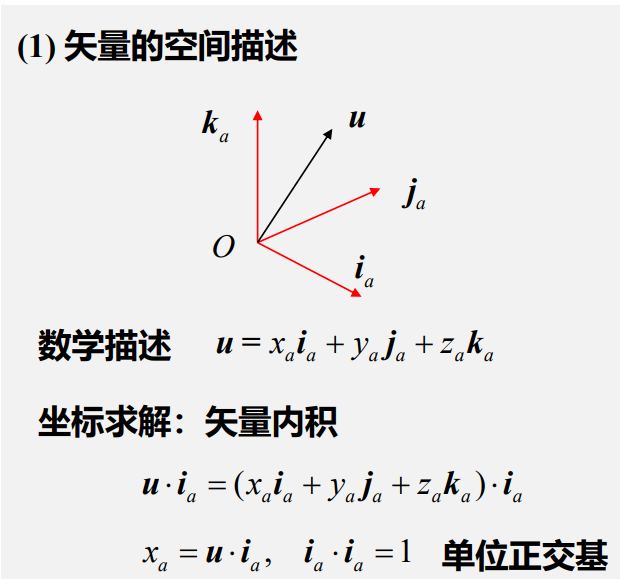
正交分解的基底思想：这个类比来源于程林老师的《现代控制理论》，程林老师尝试使用一节课给我们理清楚经典控制理论到底在干啥——其中很重要的一个点就是究竟傅里叶变换和拉普拉斯变换在干啥？
这里先从傅里叶变换来说，正如前文所讲，在信号处理中，我想从一堆混乱信号中分辨出各个$\omega$的信号的多少。这就联想到了我们从初中就开始一直干的事情——基底思想。比如我想知道在一个空间向量$\vec{u}$ 在$\vec{i}$方向上的分量有多大，我就使用$\vec{i}$为基底，$\vec{u}\cdot \vec{i}$ 做内积即可得到$\vec{u}$ 在$\vec{i}$方向上的分量大小！那么为啥可以这样做呢，就是因为在$\vec{u}$中存在的与$\vec{i}$不平行的分量，在与$\vec{i}$做点积后自然满足等于零，从而我们从$\vec{u}$中筛选出了$\vec{i}$方向的分量。
仔细想想，这其实与我们现在想干的事是一个事，那能不能找到一个类似基底的方法，也能满足将混乱的$f(x)$与之一乘之类的，就能将对应频率为$\omega$的信号筛选出来？很遗憾，没找到能有想上文那样极其简单的方式。但好在我们发现，乘上一个特定的$e^{-i\omega t}$，然后再积个分，就能筛选出来了！！！
How to Filter out $\omega$?
先从三个简单的积分式子开始：
\[\begin{equation} \int_{-\infty}^{+\infty}{\cos \left( \omega _0t \right)}\cos \left( \omega t \right)dt =\begin{cases} 0 , \omega \ne \omega _0\\ \infty ,\omega =\omega _0\\ \end{cases} \end{equation}\] \[\begin{equation} \int_{-\infty}^{+\infty}{\sin \left( \omega _0t \right)}\sin \left( \omega t \right)dt =\begin{cases} 0 , \omega \ne \omega _0\\ \infty ,\omega =\omega _0\\ \end{cases} \end{equation}\] \[\begin{equation} \int_{-\infty}^{+\infty}{\cos \left( \omega _1t \right)}\sin \left( \omega_2 t \right)dt \equiv 0 \end{equation}\]观察第一个式子和第二个式子，我们发现这不就是一个完美的“基底”？当且仅当$\omega=\omega_0$时，积分会突然变成无穷大，其余时候毫无反应，均为0。可以观看油管上的视频The intuition behind Fourier and Laplace transforms I was never taught in school (youtube.com)，图片与本文的思路灵感也是来源于此。
Scanner of $\cos(\omega t)$ & Scanner of $\sin(\omega t)$
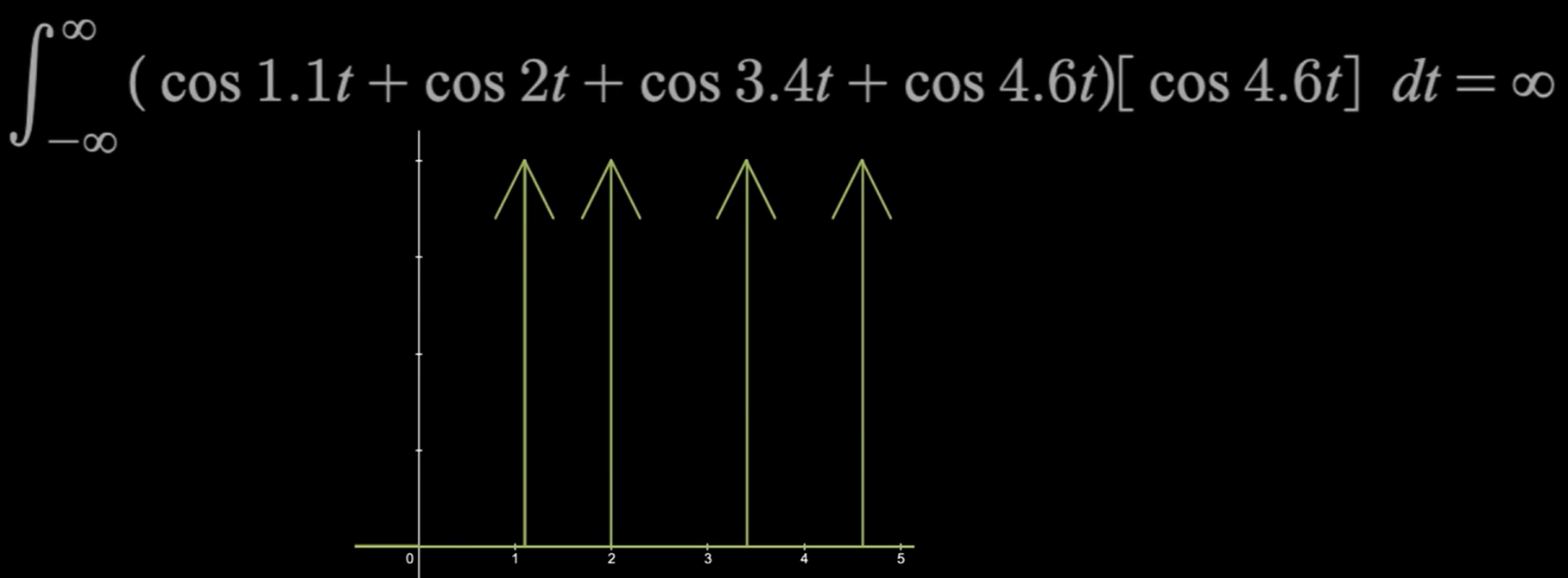
\[\int_{-\infty}^{+\infty}{f\left( t \right)}\cos \left( \omega t \right)dt\]Scanner of $\cos(\omega t)$: 视频中形象地将$cos(\omega t)$比作scanner——其实和程老师提出的“基底”的思想有异曲同工之处。当我们的$\omega$连续变化时，若被积函数$f(t)$中没有对应$\omega$的$\cos(\omega t)$时，返回0，一旦scan到相同$\omega$的$\cos(\omega t)$，立马输出尖峰信号无穷大，下面就是视频中的例子，对于前面这一长串混合输入信号，经过我们的scanner之后，遍历了横轴上的所有$\omega$，最终得到了4个对应的尖峰信号。
Scanner of $\sin(\omega t)$: 同样的道理，$\sin(\omega t)$也可以作为一个同样的scanner，来检测输入$f(t)$中的特定$\omega$的$\sin(\omega t)$信号。
\[\int_{-\infty}^{+\infty}{f\left( t \right)}\sin \left( \omega t \right)dt\]其实这样就基本找到合适的“基底”了，而且也能一定程度上理解为何任意一个函数都能分解成$\cos $与$\sin$的线性叠加（不严谨哈，数学不好不要苛求）。但数学家们肯定觉得这样还不够简洁啊，我不想为这两个“基底”分开写两个式子，多麻烦。这个时候就要感谢我们伟大的欧拉公式。将其合二为一：
\[e^{i\omega t}=\cos (\omega t) +i\sin (\omega t)\]Ultimate Scanner
这个时候就成就了我们的终极scanner，合二为一也就是我们现在看到的广义傅里叶变换，注意这里我们用的是$-\omega t$，这里我确实不清楚为啥选了负的，好像国外也有用正的教材，反正不影响本质结果：
\[F\left( \omega \right) =\mathscr{F} \left[ f\left( t \right) \right] =\int_{-\infty}^{+\infty}{f\left( t \right) e^{-i\omega t}dt}=\int_{-\infty}^{+\infty}{f\left( t \right) [\cos (\omega t) -i\sin (\omega t)]dt}\]这个时候就会有人心里开始犯嘀咕了，我这样轻易的把两个scanner叠加在一起了，它们两个之间的结果不会相互干扰吗？巧了，好就好在，还真不会！还是举个最简单的例子，当$f(x)=\cos(\omega_1 t)+\sin(\omega_2 t)(\omega_1\ne \omega_2)$时，
\[F\left( \omega \right) =\int_{-\infty}^{+\infty}{[\cos(\omega_1 t)+\sin(\omega_2 t)] e^{-i\omega t}dt}=\int_{-\infty}^{+\infty}{[\cos(\omega_1 t)+\sin(\omega_2 t)][\cos (\omega t) -i\sin (\omega t)]dt}\]当$\omega=\omega_1$时，$\int_{-\infty}^{+\infty}{\cos \left( \omega _1t \right)}\cos \left( \omega t \right)dt=\infty$，检查到$\cos(\omega_1 t)$信号，此时式子中剩余3项都一定会等于0，这有=由最早列出的3条式子保证：
\[\int_{-\infty}^{+\infty}{\sin \left( \omega _2t \right)}\cos \left( \omega t \right)dt=\int_{-\infty}^{+\infty}{-i\cos \left( \omega _1t \right)}\sin \left( \omega t \right)dt=\int_{-\infty}^{+\infty}{-i\sin \left( \omega _2t \right)}\sin \left( \omega t \right)dt=0\]如此一来，我们也就证明了一旦检测到一个信号，其他所有的scanner都会“自觉闭麦”，所以不会出现互相干扰的情况，这下我们就可以在一个积分中完美检测$\cos(\omega t)$与$\sin(\omega t)$信号啦。
Further Discussion
Why $\infty$ disappear?
按照我们刚刚分析的那样，是不是感觉傅里叶变换亲切了很多？但不知道你发现没有——按照上面那样的想法，傅里叶变换后的结果应该只有0或者$\infty$这2种情况呀，为啥我们平时看到的往往不是这样呢？这在视频The intuition behind Fourier and Laplace transforms I was never taught in school (youtube.com)中也有动画讲解，会比我书面描述直管得多，可以科学上网跳转观看。
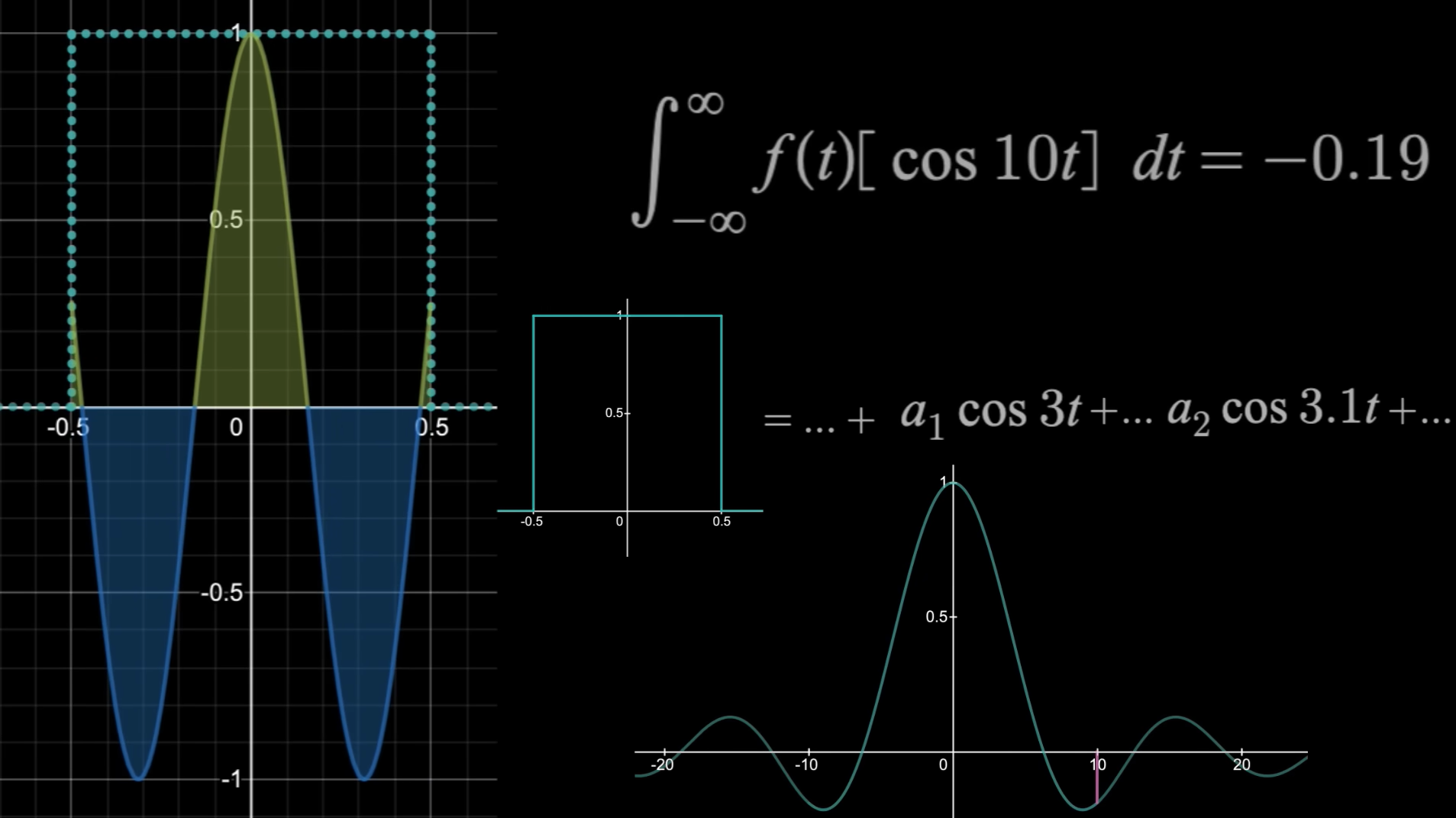
举个栗子，在我们对方波函数进行傅里叶变换时，因为此方波是偶函数，乘上$\sin$的积分都等于0，简单起见，我们可以只要使用$\cos(\omega t)$进行检测即可，与傅里叶变换等价。上图右下角即为傅里叶积分的值随着$\omega$变化的返回值，我们发现与之前简单的例子不同——这里没有尖峰信号，也没有无穷，而是有限值的连续函数。
这是为啥，难道我们刚刚的结论错了？其实不然。没有返回$\infty$的原因在于，这个$\infty$的功力被另一位“江湖扫地僧”大大削弱，就是$\cos(\omega t)$前面的系数$a$，如果$\int_{-\infty}^{+\infty}{f\left( t \right)}\cos \left( 10 t \right)dt=-0.19$,我们可以知道的是，这个方波信号$f(t)$中一定有$\cos(10t)$，但是呢，不多，可以说是很少很少，其前面的系数$a\rightarrow 0$，我们学过数学分析都知道，一个趋近于0的数乘上$\infty$是可以等于任意常数的，这就解释清除了为什么没有出现无穷的返回值。
另一个问题就是为什么是连续的？那更好解释，说明方波信号中含有的$\cos(\omega t)$信号的$\omega$也是连续的，嘿嘿，我几乎都有（除了返回值为0的$\omega$），但都不太多，以至于返回值是连续的有限值。
Why return Complex Number?
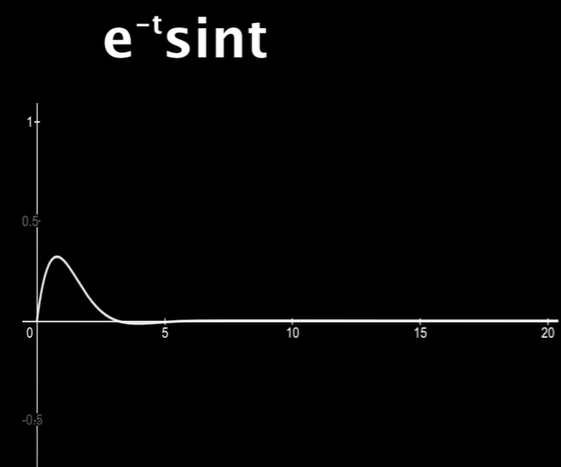
还有另一个问题就是，往往积分输出的值并不是一个简单的实数，多数情况下应该是个复数。拿一个非常好的例子来看（注意哦，这里为后面的拉普拉斯变换做铺垫），如图
\(x\left( t \right) =\begin{cases} 0,t<0\\ e^{-t}\sin t,t\geqslant 0\\ \end{cases}\) 可以看到，就当$\omega=1$时，返回的结果就是$\frac{1}{5}-i\frac{2}{5}$，这就是说明其中既有$\cos t$也有$\sin t$。其实很容易理解的就是返回值的实数部分对应的是$\cos$信号，虚数部分对应的就是$\sin$信号。
Laplace Transform
理解了上面一大坨关于傅里叶变换的知识，对于拉普拉斯变换也就迎刃而解了，所以关于拉普拉斯变换的讲解部分不会那么长。
Definition
\[F\left( s \right) =\mathscr{L} \left[ f\left( t \right) \right] =\int_{0}^{+\infty}{f\left( t \right) e^{-st}dt}\]The Link between Laplace Trandform & Fourier Transform
\[F\left( s \right) =\int_0^{+\infty}{f\left( t \right) e^{-st}dt}=\int_0^{+\infty}{f\left( t \right) e^{-\left( \alpha +i\omega \right) t}dt}=\int_0^{+\infty}{\left[ f\left( t \right) e^{-\alpha t} \right] e^{-i\omega t}dt}\]我对拉普拉斯变换中的$s$进行实部虚部分离$s=\alpha+i\omega$，然后我如果把$f(t)$与$e^{-\alpha t}$结合成一个函数，形式是不是就和之前的傅里叶变换极其一致了？
但要注意的是，拉普拉斯变换与傅里叶变换最大的一个不同在于积分下界的不同，拉普拉斯变换是$0\sim+\infty$，而不是$-\infty\sim+\infty$！这其实是因为在工程上，很多信号在$t=0$之前没有意义，我们也不去关心，所以才出现了这种形式方便使用。当然在数学上还是存在双边拉普拉斯变换的说法的，这个我们不做讨论。
What’s Laplace Transform doing?
What’s $e^{-\alpha t}$ doing?
从上面可以看出，如果把$f(t)e^{-\alpha t}$看做一个函数整体的话，拉普拉斯变换还是可以通过后面的$e^{-\omega t}$实现对$\cos(\omega t)$和$\sin(\omega t)$的scan。现在需要关注的是多出来的$e^{-\alpha t}$是干嘛的。
其实很简单，$e^{-\alpha t}$仍然起到一个scanner的作用，只不过这次scan的对象是——$e^{\alpha t}$！虽然傅里叶很好用，可以完美地对 $\sin$ 与 $\cos$ 进行扫描，但追求完美的数学家肯定不满足于此，寻思着如果同时还能对 $e^{\alpha t}$ 进行扫描该多好——直接在积分时再乘上一个 $e^{-\alpha t}$ ！我们来分析一下，这里还是使用上面的例子，
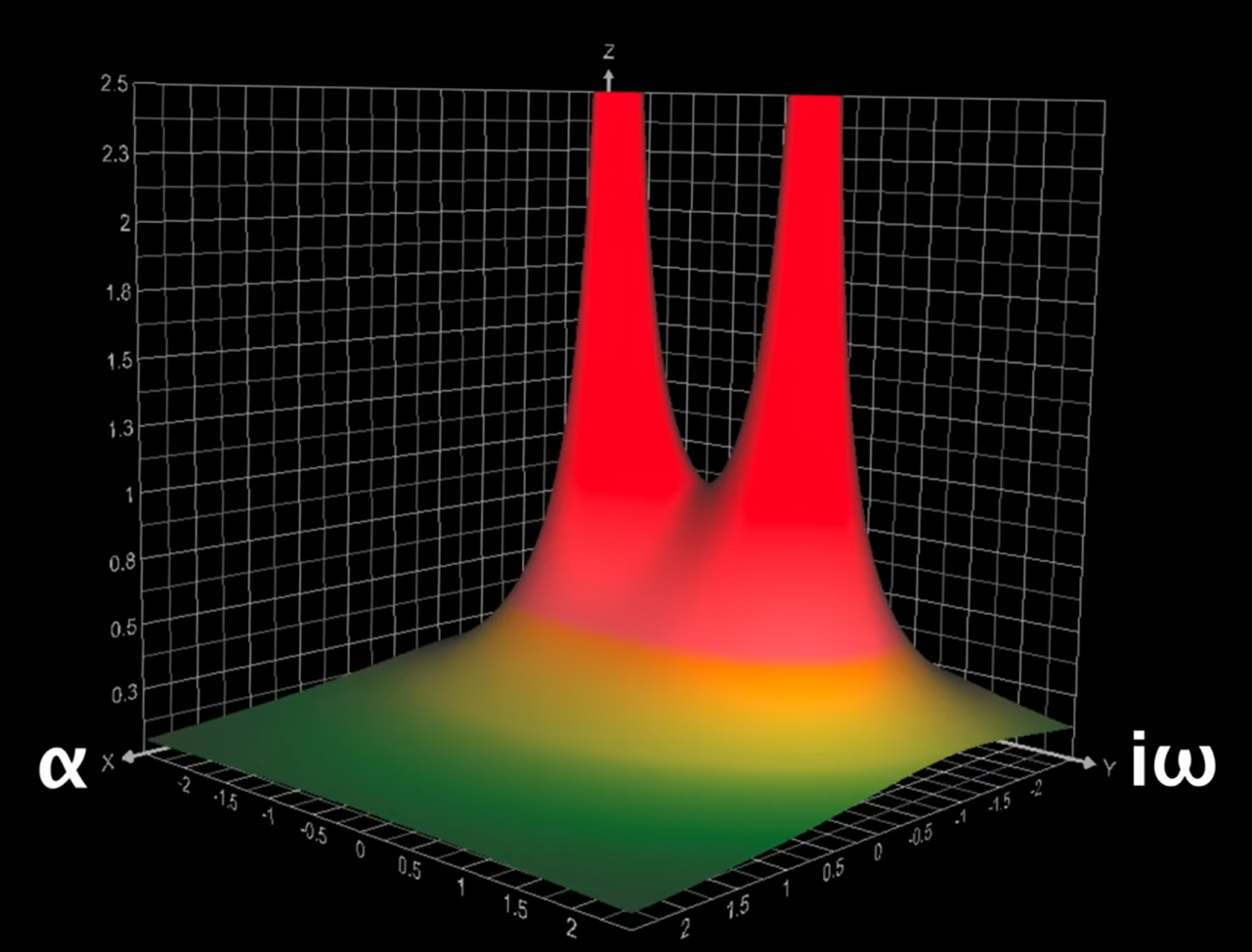
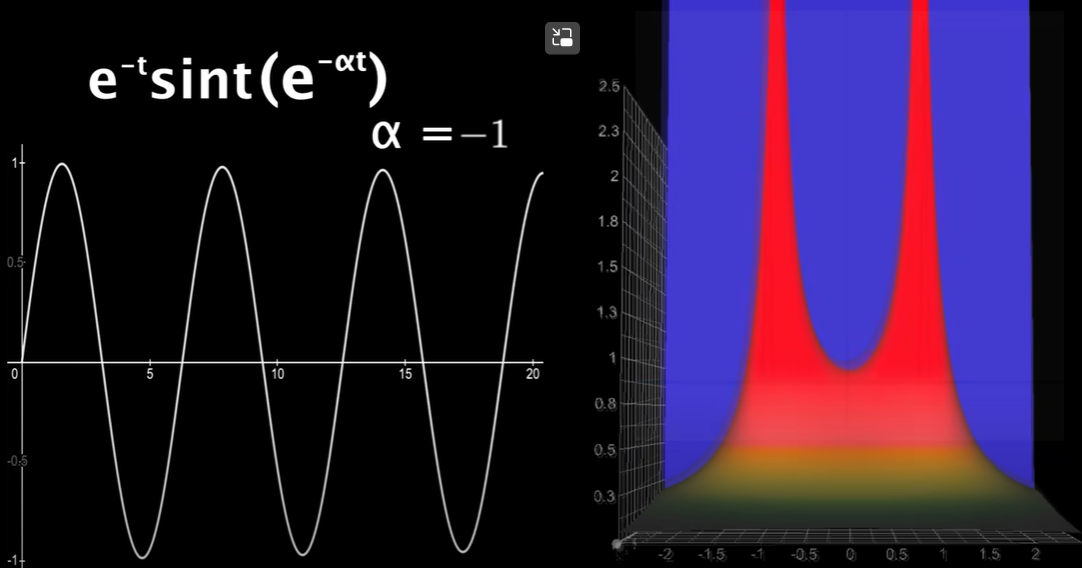
\[f(t)=e^{-t}\sin t,(when \ t>0,else\ f(t)=0)\] \[F\left( s \right) =\int_0^{+\infty}{\left[ e^{-t}\sin t\ e^{-\alpha t} \right] e^{-i\omega t}dt}\]
我们可以绘制出$f(t)$拉普拉斯变换后的立体图像，如下图，可以看到有两个趋于$\infty$的尖峰，这其实就是我们在拉普拉斯变换中所关注的点，或者说就是scaner起作用的地方
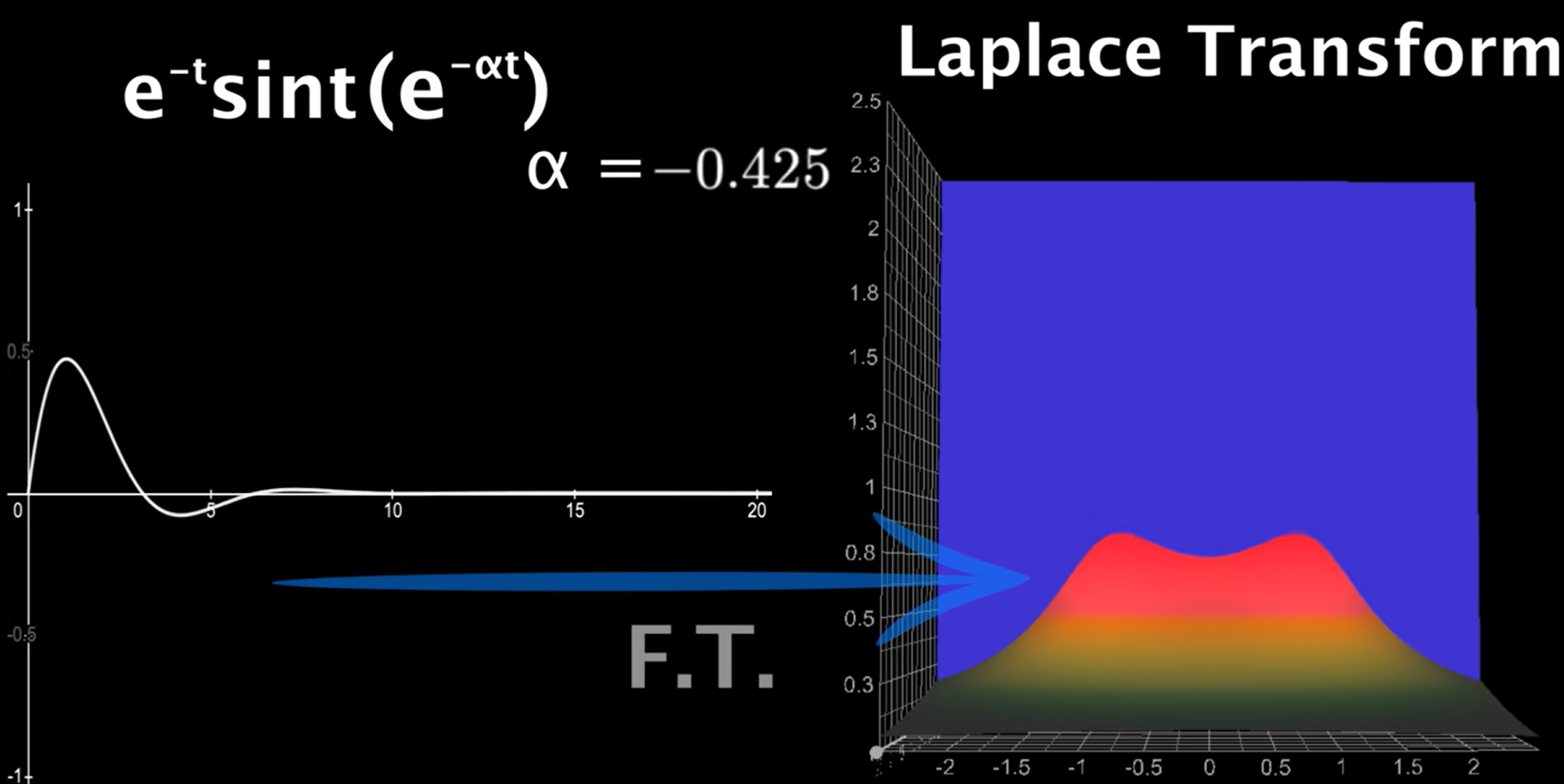
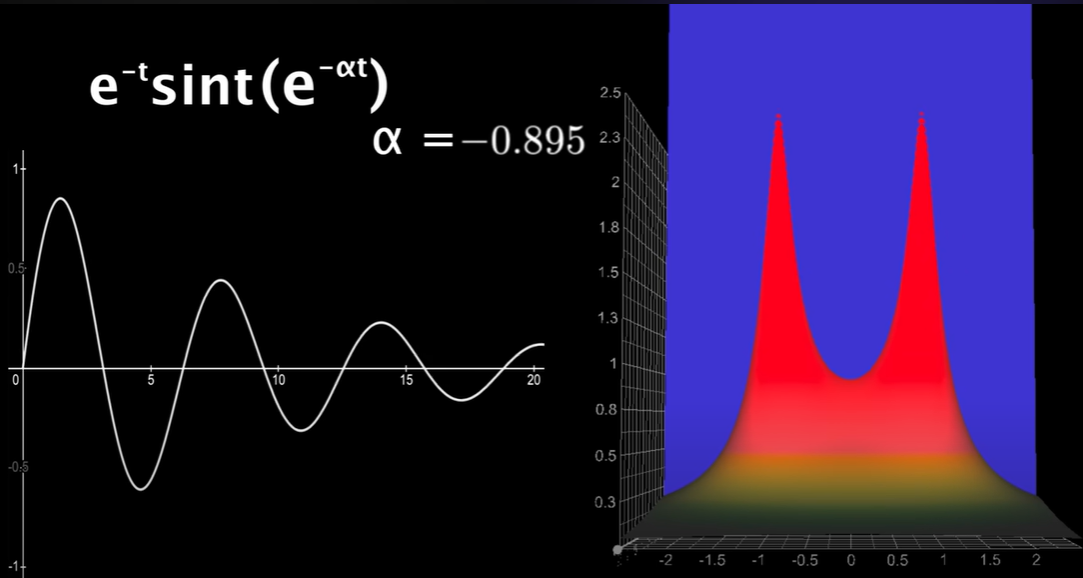
我们现在来模拟图像生成的过程，为了方便起见，干脆直接把$e^{-\alpha t}$乘到$f(t)$上，之后我们就可以把拉普拉斯变换转换成傅里叶变换了，下面三张图展现了随着$\alpha$增大，积分函数的变化过程。
最为需要关注的就是第三张图，此时$\alpha=-1$，正好使得$e^{-\alpha t}$与前面的$e^{-t}$相互抵消了！此时我们就相当于在使用$e^{-i\omega t}$给剩下的$\sin(t)$scan，也就是傅里叶变换。而回想刚刚的知识，此时此刻当$\omega=\pm1$时，将检测到前方的$\sin(t)$，返回$\infty$！！！（注意：在这里绘制的返回值都是复数的模值）这也就解释了两个尖峰的来源。
By the way，需要注意的是，当$\alpha<-1$时，其实拉普拉斯变换是没有意义的。想想一下此时等效成傅里叶变换之后，前部的被积函数为$\sin(t)e^{(-\alpha+1)t}$，这个函数显然是不收敛的，我们并不能得到收敛的积分值。
About poles
这两个尖峰对应的复平面坐标，其实就是所谓的“极点”！（pole）我们在工程上使用拉普拉斯变换，其实大部分情况下都只是关心这个极点所在的位置！极点的坐标$(\alpha,\omega)$正是反映了原函数$f(t)$中含有的$e^{\alpha t}$与$sin(\omega t)$或者是$\cos(\omega t)$。一旦通过拉普拉斯变换这个超级scanner（双料特工）找到尖峰对应的极点，就可以随之确定$f(t)$的形式如下所示：
\(f(t)=Ae^{\alpha t}[B\cos(\omega t)+C\sin(\omega t)]\) 嘿嘿，大功告成！这样在工程上不就能判断一个系统返回信号可不可用，收不收敛了吗。
这个时候有的同学就灵机一动，开始质疑了：你明明是通过已有的$f(t)$拉普拉斯变换积分后才知道极点的位置，你现在又拿这个来判断原函数$f(t)$的形式？这不是闲着没事干多此一举吗?
非也非也，其实我们在应用中，往往是不知道$f(t)$的具体式子的，也不是通过直接对$f(t)$拉普拉斯变换得到的$F(s)$。往往是对已有的输入信号和系统的传递过程方乘求解时，就已经进行了拉普拉斯变换，进而解出$F(s)$的式子，从而确定极点，再确定$f(t)$的形式。
这个时候有聪明的童鞋又要问了，为啥都列出$t$为变量的方程了，直接解不久完事了？？？不就得到$f(t)$了吗？？？巧了，大部分情况下还真不好解，更别忘了咱们是数学不好的工程师不是数学家！更不会解！但恰恰拉普拉斯变换后有一些奇妙的性质，使得我们这些“笨鸟”也能求解，且看下面揭晓：
Why We Use the Laplace Transform in Classical Control Theory?
Perfect derivative properties
其实上图展示的就是拉普拉斯变换完美的求导性质，又得益于在工程上，往往$t=0$时，各个变量的值均为0（不是0的时候需要特别注意不能随意消去后面的项），这就使得拉普拉斯变换能轻松的将复杂的微分方程转化为初中生的多项式计算！这样就可以轻松地解出我们所要的变量$y(s)$啦！
Why we always care about poles?
先讨论一下，一个形如
\(f(t)=Ae^{\alpha t}[B\cos(\omega t)+C\sin(\omega t)]\) 的输出信号，在什么条件下才能算是稳定？其实很简单，条件只有一个—— $\alpha<0$，这样就能保证当$t\rightarrow+\infty$时，$f(t)\rightarrow 0$。无论如何，当$t\rightarrow+\infty$，一个系统输出的信号总得归于平静吧，你不能说信号一直存在，更不可能说愈演愈烈了。
因此，我们其实只需要保证极点在虚轴的左侧，就可以说输出信号是稳定的啦，也就是系统是稳定的。
我们在经典控制理论中，为了省去每次列方程求解的烦恼，直接选择使用传递函数表述一个系统，拒绝重复计算！大多数情况下，我们会把系统的输出$C(s)$表示为：
\[C(s)=\frac{M(s)}{D(s)}R(s)\]其中$R(s)$为输入信号，$M(s)$为输入端算子式，$D(s)$为输出端算子是，也就是常说的闭环特征式子。其实这些名词都不是很重要，我们现在就是想知道$C(s)$对应的$f(t)$究竟是不是$\alpha<0$？其实就是知道极点的位置，也就是知道上面的式子何时取得尖峰$\infty$？这里不妨换一个思路，使得$C(s)\rightarrow \infty$，不就是等价于使得$D(s)\rightarrow0$ 吗？（这其实也是极点的另一个定义）。于是乎，经典控制理论就围绕如何判断使得$D(s)=0$时$s$的位置开始了大讨论，让我们一起来回忆一下经典控制理论中的各种方法：
时域分析法：
最常用的三个：古尔维茨判据、林纳德-奇帕特判据、劳斯判据，其实都是通过判断系统特征方程$D(s)$的形式与系数来做到不解方程判断零点（极点）位置。
复域分析法——根轨迹法
根轨迹法就是通过很多结论与技巧，画出特征方程的根的轨迹，来直观判断极点在复平面位置。
频域分析法——频率法
最常用的是奈氏判据，实际上也是根据幅角原理与开环频率特性曲线，来判断是否在虚轴右侧无零点，如果没有，则判定为稳定。
总而言之，到头来都是数学家借助各种数学方法总结成了各种tricks来确定极点是不是在复平面左侧，来供我们这些数学不好的工程师使用，就形成了经典控制理论。
Afterword
在程林老师的启发下，才决定重新学习理解傅里叶变换、拉普拉斯变换以及经典控制理论，提笔写下这篇笔记。前后断断续续写了两周完成，在此之间确实理清了很多之前没有搞懂的问题。但限于实力不足，中间夹杂了太多的废话，肯定还不乏逻辑上数学上的错误，如果有他人看到，敬请原谅！也欢迎留言告知错误！不胜感激！